核方法（Kernel Methods）

核方法（Kernel Methods）

支持向量机（SVM）是机器学习中一个常见的算法，通过最大间隔的思想去求解一个优化问题，得到一个分类超平面。对于非线性问题，则是通过引入核函数，对特征进行映射（通常映射后的维度会更高），在映射之后的特征空间中，样本点就变得线性可分了。

核方法的示意图如下：

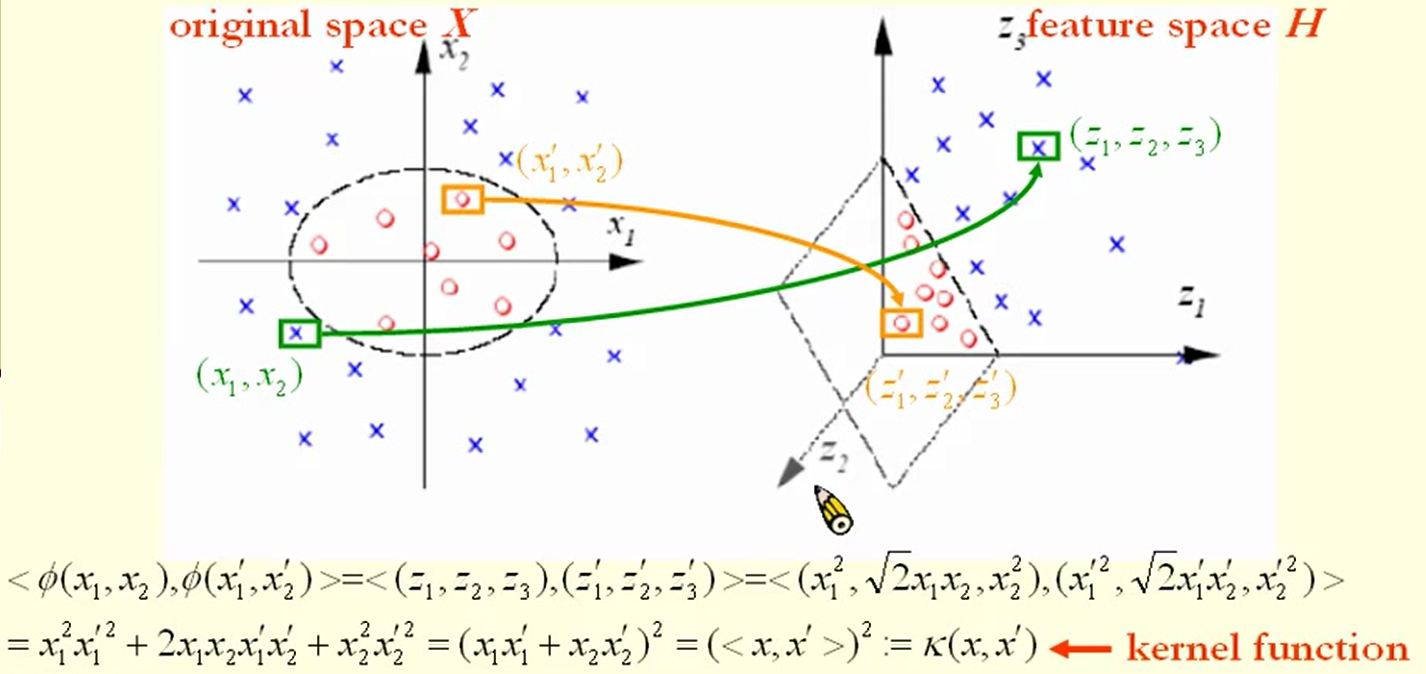
上图中左边表示的是原始特征空间，在原始特征空间中，我们无法用直线（平面）来将两类点分开，但是却可以用圆来进行分割。右边表示的通过对原始样本点进行映射（从二维映射到三维）得到的新的样本点。可以看到在新的特征空间中，两类样本点可以通过一个平面分开。

核方法的应用除了在支持向量机之外，在感知机上，对应<xi,xj>的位置利用核函数代替，就有了核感知机；同理还有核聚类，核PCA等。

常用的核函数

除了上述的核函数之外，还有Sigmoid核函数，并且将核函数进行线下组合，也仍然是核函数。

核函数定义

知道了核函数的应用以及有哪些核函数之后，我们来看看，什么样的函数能作为核函数，是不是我们能自己构造核函数。

核函数一个有效的判断方式是通过Mercer定理：

简单的说就是，判断核函数K对应的Gram矩阵是否是半正定的。但是值得注意的是，Mercer定理不是核函数必要条件，只是一个充分条件，也就是说还有不满足Mercer定理的函数也可以是核函数。

参考：

1、机器学习中的核方法（Kernel Method）

2、支持向量机（三）核函数