剪邮票--蓝桥杯--dfs--思路超清晰

剪邮票

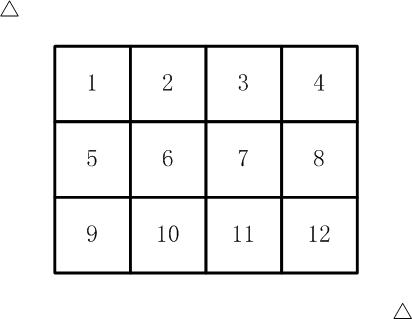
如【图1.jpg】, 有12张连在一起的12生肖的邮票。
现在你要从中剪下5张来，要求必须是连着的。
（仅仅连接一个角不算相连）
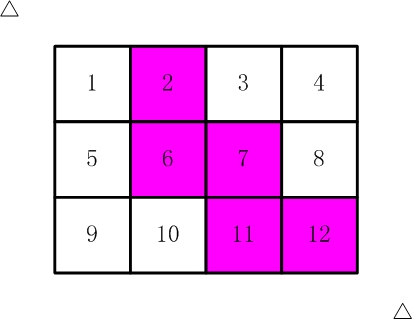
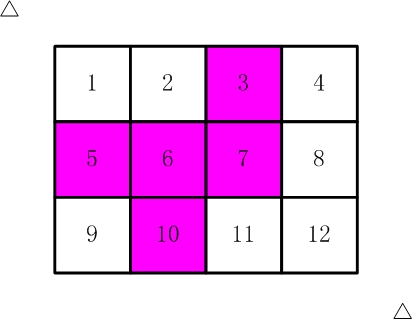
比如，【图2.jpg】，【图3.jpg】中，粉红色所示部分就是合格的剪取。

请你计算，一共有多少种不同的剪取方法。

题解：用for循环把1~12每一个点作为搜索起点去dfs次，已经作为搜索起点的点不能再被dfs过程中枚举

所得的最后结果再加2；

为什么要加2？
因为我这里搜索的是由起点不断外延伸的，所以cnt只包含了线性连通的情况
这里还有两种放射状连通的情况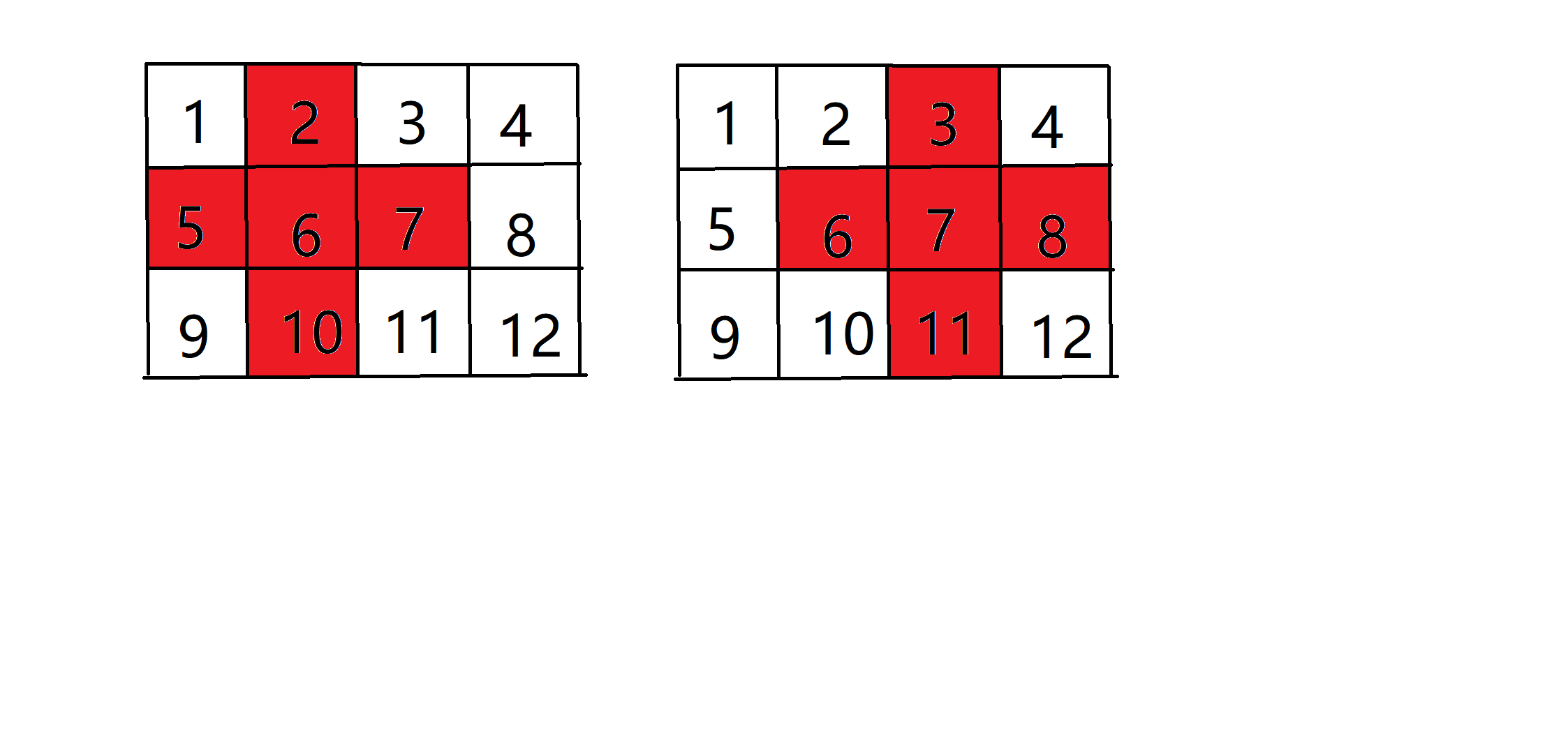

答案：116

#include<iostream>
#include<string.h>
using namespace std;
int a[][],star[],vis[][],dir[][]={{,},{-,},{,},{,-}};
int cnt=;
int check(int x,int y)
{
    if(x>=&&x<&&y>=&&y<)
        return ;
    else
        return ;
}
void dfs(int x,int y,int dep)
{
    if(dep==)
    {
        cnt++;
        return;
    }
    else
    {
        for(int i=;i<;i++)
        {
            int tx,ty;
            tx=x+dir[i][];
            ty=y+dir[i][];
            if(check(tx,ty)&&!vis[tx][ty]&&!star[a[tx][ty]])//在棋盘内/可以剪/这个点没有作为搜索起点使用过
            {
                vis[tx][ty]=;
                dfs(tx,ty,dep+);
                vis[tx][ty]=;
            }

        }
    }

}
int main()
{
    int n=;
    for(int i=;i<;i++)
    {
        for(int j=;j<;j++)
            a[i][j]=n++;
    }
    for(int i=;i<;i++)
    {
        for(int j=;j<;j++)
        {
            dfs(i,j,);
            star[a[i][j]]=;//标记搜索起点，避免重复
        }
    }
    cout<<cnt+<<endl;//为什么要加2？
                      //因为我这里搜索的是由起点不断外延伸的，所以cnt只包含了线性连通的情况
                      //这里还有两种放射状连通的情况
}