HDU1401 BFS

Solitaire

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 4368    Accepted Submission(s): 1324

Problem Description

Solitaire is a game played on a chessboard 8x8. The rows and columns of the chessboard are numbered from 1 to 8, from the top to the bottom and from left to right respectively.

There are four identical pieces on the board. In one move it is allowed to:

> move a piece to an empty neighboring field (up, down, left or right),

> jump over one neighboring piece to an empty field (up, down, left or right).

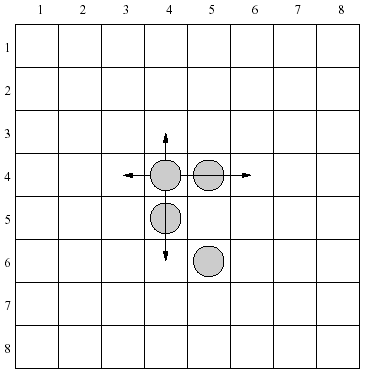
There are 4 moves allowed for each piece in the configuration shown above. As an example let's consider a piece placed in the row 4, column 4. It can be moved one row up, two rows down, one column left or two columns right.

Write a program that:

> reads two chessboard configurations from the standard input,

> verifies whether the second one is reachable from the first one in at most 8 moves,

> writes the result to the standard output.

 

Input

Each of two input lines contains 8 integers a1, a2, ..., a8 separated by single spaces and describes one configuration of pieces on the chessboard. Integers a2j-1 and a2j (1 <= j <= 4) describe the position of one piece - the row number and the column number respectively. Process to the end of file.

 

Output

The output should contain one word for each test case - YES if a configuration described in the second input line is reachable from the configuration described in the first input line in at most 8 moves, or one word NO otherwise.

 

Sample Input

4 4 4 5 5 4 6 5

2 4 3 3 3 6 4 6

 

Sample Output

YES

 

Source

Southwestern Europe 2002

题意：

问在8步之内能否从前一个状态到后一个状态，棋子只能上下左右走或者如图中的方式走（跳过相邻的一个棋子）。

代码：

 /*
 用bool开一个8维数组vis记录状态是否走过，很容易超内存，尽量少开数组减少内存。
 */
 #include<iostream>
 #include<cstring>
 #include<queue>
 using namespace std;
 bool vis[][][][][][][][];
 bool mp[][];
 int dir[][]={,,,,-,,,-};
 struct Lu
 {
     int x[],y[],cnt;
 }L3;
 bool chak(Lu L)
 {
     for(int i=;i<;i++){
         if(!mp[L.x[i]][L.y[i]])
             return ;
     }
     return ;
 }
 bool nice(Lu L)
 {
     for(int i=;i<;i++){
         if(L.x[i]>||L.x[i]<||L.y[i]>||L.y[i]<)
             return ;
     }
     if(vis[L.x[]][L.y[]][L.x[]][L.y[]][L.x[]][L.y[]][L.x[]][L.y[]])
         return ;
     return ;
 }
 bool empt(Lu L,int k)
 {
     for(int i=;i<;i++){
         if(i==k) continue;
         if(L.x[k]==L.x[i]&&L.y[k]==L.y[i])
             return ;
     }
     return ;
 }
 bool bfs()
 {
     Lu L2;
     queue<Lu>q;
     q.push(L3);
     while(!q.empty()){
         L2=q.front();
         q.pop();
         if(chak(L2)) return ;
         if(L2.cnt>=) continue;
         for(int i=;i<;i++){
             for(int j=;j<;j++){
                 L3=L2;
                 L3.x[i]=L2.x[i]+dir[j][];
                 L3.y[i]=L2.y[i]+dir[j][];
                 if(!nice(L3)) continue;
                 if(empt(L3,i)){
                     vis[L3.x[]][L3.y[]][L3.x[]][L3.y[]][L3.x[]][L3.y[]][L3.x[]][L3.y[]]=true;
                     L3.cnt++;
                     q.push(L3);
                 }
                 else{
                     L3.x[i]=L3.x[i]+dir[j][];
                     L3.y[i]=L3.y[i]+dir[j][];
                     if(!nice(L3)) continue;
                     if(empt(L3,i)){
                         vis[L3.x[]][L3.y[]][L3.x[]][L3.y[]][L3.x[]][L3.y[]][L3.x[]][L3.y[]]=true;
                         L3.cnt++;
                         q.push(L3);
                     }
                 }
             }
         }
     }
     return ;
 }
 int main()
 {
     int x,y;
     while(cin>>x>>y){
         x--;y--;
         memset(vis,false,sizeof(vis));
         memset(mp,false,sizeof(mp));
         L3.x[]=x;L3.y[]=y;
         for(int i=;i<;i++){
             cin>>x>>y;
             x--;y--;
             L3.x[i]=x;L3.y[i]=y;
         }
         vis[L3.x[]][L3.y[]][L3.x[]][L3.y[]][L3.x[]][L3.y[]][L3.x[]][L3.y[]]=true;
         for(int i=;i<;i++){
             cin>>x>>y;
             x--;y--;
             mp[x][y]=true;
         }
         L3.cnt=;
         int flag=bfs();
         if(flag) cout<<"YES\n";
         else cout<<"NO\n";
     }
     return ;
 }