5 Logistic回归（二）

5.2.4 训练算法：随机梯度上升

梯度上升算法：在每次更新回归系数时都需要遍历整个数据集，在数十亿样本上该算法复杂度太高。

改进方法：随机梯度上升算法：一次仅用一个样本点更新回归系数。

由于可以在新样本到来时对分类器进行增量式更新，因此随机梯度上升算法是一个在线学习算法。与“在线学习”相对应，一次处理所有数据被称作“批处理”。

#5-3:随机梯度上升算法
def stocGradAscent0(dataMatrix, classLabels):
    m, n = shape(dataMatrix)
    alpha = 0.01
    weights = ones(n)
    for i in range(m):
        h = sigmoid(sum(dataMatrix[i] * weights))
        error = classLabels[i] - h
        weights = weights + alpha * error * dataMatrix[i]
    return weights

随机梯度上升与梯度上升的区别：1.前者变量h和error都是数值，后者都是向量；2.前者没有矩阵转换过程，所有变量数据类型都是Numpy数组。

拟合效果没有梯度上升算法完美。这里的分类器错分了三分之一的样本。梯度上升算法的结果是在整个数据集上迭代了500次才得到的。

判断优化算法优劣的可靠方法：看它是否收敛，也就是说参数是否达到稳定值，是否不断地变化。

对此，在程序5-3中随机梯度上升做些修改，使其在整个数据集上运行200次。最终绘制的三个回归系数变化情况如下图：

图5-6

X2经过50次迭代达到稳定值，但X0和X1需要更多次迭代。产生这种现象原因：存在一些不能正确分类的样本点（数据集并非线性可分），在每次迭代时会引发系数的剧烈改变。我们希望算法能避免来回波动，从而收敛到某个值。另外，收敛速度也需要加快。

#5-4:改进的随机梯度上升算法
def stocGradAscent1(dataMatrix, classLabels, numIter = 150):
    m, n = shape(dataMatrix)
    weights = ones(n)
    for j in range(numIter):#j迭代次数
        dataIndex = range(m)
        for i in range(m):#i样本点下标
            alpha = 4/(1.0 + j + i) + 0.01#alpha每次迭代时需要调整
            randIndex = int(random.uniform(0, len(dataIndex)))#randIndex编号:样本在矩阵中的位置
            h = sigmoid(sum(dataMatrix[randIndex] * weights))
            error = classLabels[randIndex] - h
            weights = weights + alpha * error * dataMatrix[randIndex]
            del(dataIndex[randIndex])
    return weights

改进之处：1.alpha每次迭代时需要调整，缓解上图数据波动或者高频波动。虽然alpha随迭代次数不断减小，但永远不会小于0，因为存在常数项（0.01）。这样做的原因：保证多次迭代后新数据仍有一定的影响。alpha每次减少1/(j+i)，j是迭代次数，i是样本点下标。当j<<max(i)，alpha就不是严格下降。2.通过随机选取样本更新回归系数，减少周期性波动。具体实现方法与第3章类似，每次随机从列表中选出一个值，然后从列表中删掉该值（再进行下一次迭代）。

图5-7

该方法比采用固定的alpha收敛速度更快。主要归功于：1.stocGradAscent1()的样本随机机制避免周期性波动；2.stocGradAscent1()收敛更快。这次仅对数据集做了20次遍历，而之前的方法是500次。

5.3 示例：从疝气病症预测病马的死亡率

(1)收集数据

(2)准备数据

(3)分析数据

(4)训练算法：使用优化算法，找到最佳系数

(5)测试算法：为了量化回归的效果，需要观察错误率。根据错误率决定是否退到训练阶段，通过改变迭代次数和步长等参数得到更好的回归系数。

(6)使用算法

5.3.1 准备数据：处理数据中的缺失值

预处理需要做2件事：

1.缺失值必须用一个实数值来替换，因为Numpy类型不允许包含缺失值。这里选择0替换所有缺失值，恰好适用于Logistic回归。这样做原因：需要一个在更新时不会影响系数的值。

2.如果数据集中类别标签已缺失，则丢弃该数据。

5.3.2  测试算法：用Logistic回归进行分类

使用Logistic回归需要做的事情：将测试集上每个特征向量乘以最优化方法得来的回归系数，再将该乘积结果求和，最后输入到Sigmoid函数中。如果对应的Sigmoid值大于0.5则预测类别标签为1，否则为0.

#5-5:Logistic回归分类函数
def classifyVector(inX, weights):#(特征向量，回归系数)
    prob = sigmoid(sum(inX * weights))
    if prob > 0.5: return 1.0
    else: return 0.0

def colicTest():#打开测试集、训练集
    frTrain = open('horseColicTraining.txt')
    frTest = open('horseColicTest.txt')
    trainingSet = []; trainingLabels = []
    for line in frTrain.readlines():
        currLine = line.strip().split('\t')
        lineArr = []
        for i in range(21):#0-20:20个特征，1个类标签
            lineArr.append(float(currLine[i]))
        trainingSet.append(lineArr)
        trainingLabels.append(float(currLine[21]))
    trainWeights = stocGradAscent1(array(trainingSet), trainingLabels, 500)#计算回归系数

    errorCount = 0; numTestVec = 0.0
    for line in frTest.readlines():#导入测试集，计算分类错误率
        numTestVec += 1.0
        currLine = line.strip().split('\t')
        lineArr = []
        for i in range(21):
            lineArr.append(float(currLine[i]))
        if int(classifyVector(array(lineArr), trainWeights)) != int(currLine[21]):
            errorCount += 1
    errorRate = float(errorCount) / numTestVec
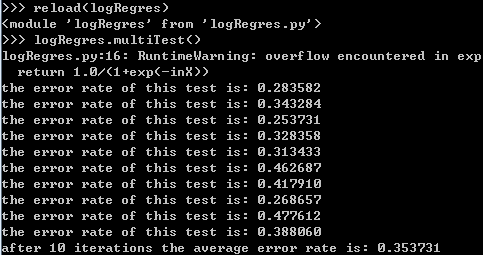
    print "the error rate of this test is: %f" % errorRate
    return errorRate

def multiTest():#调用colicTest()10次求平均值
    numTests = 10; errorSum = 0.0
    for k in range(numTests):
        errorSum += colicTest()
    print "after %d iterations the average error rate is: %f" % (numTests, errorSum/float(numTests))

5.4 总结

Logistic回归的目的是寻找一个非线性函数sigmoid的最佳拟合参数，求解过程可以由最优化算法来完成。在最优化算法中，最常用的就是梯度上升算法，而梯度上升算法又可以简化为随机梯度上升算法。

随机梯度上升算法和梯度上升算法的效果相当，但占用更少的计算资源。此外，随机梯度是一种在线算法，可以在数据到来时就完成参数的更新，而不需要重新读取整个数据集来进行批处理运算。