leetcode_question_62 Unique Paths

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

How many possible unique paths are there?

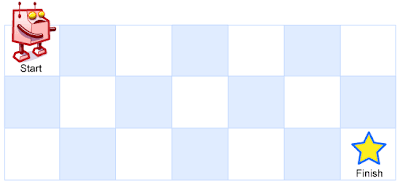
Above is a 3 x 7 grid. How many possible unique paths are there?

Note: m and n will be at most 100.

class Solution {
public:
    int dp[101][101];
    int uniquePaths(int m, int n) {
        // Start typing your C/C++ solution below
        // DO NOT write int main() function
    	if(m < 1 || n < 1)return 0;

		for(int i = 1; i <= m; ++i){
			dp[i][1] = 1;
		}
		for(int j = 1; j <= n; ++j){
			dp[1][j] = 1;
		}

		for(int i = 2; i <= m; ++i)
			for(int j = 2; j <= n; ++j)
				dp[i][j] = dp[i][j-1]+dp[i-1][j];

		return dp[m][n];
    }
};