[bzoj3244] [洛谷P1232] [Noi2013] 树的计数

Description###

我们知道一棵有根树可以进行深度优先遍历（DFS）以及广度优先遍历（BFS）来生成这棵树的DFS序以及BFS序。两棵不同的树的DFS序有可能相同，并且它们的BFS序也有可能相同，例如下面两棵树的DFS序都是1 2 4 5 3，BFS序都是1 2 3 4 5

现给定一个DFS序和BFS序，我们想要知道，符合条件的有根树中，树的高度的平均值。即，假如共有K棵不同的有根树具有这组DFS序和BFS序，且他们的高度分别是h1,h2,...,hk，那么请你输出

(h1+h2..+hk)/k

Input###

有3行。

第一行包含1个正整数n，表示树的节点个数。

第二行包含n个正整数，是一个1~n的排列，表示树的DFS序。

第三行包含n个正整数，是一个1~n的排列，表示树的BFS序。

输入保证至少存在一棵树符合给定的两个序列。

Output###

仅包含1个实数，四舍五入保留恰好三位小数，表示树高的平均值。

Sample Input###

5

1 2 4 5 3

1 2 3 4 5

Sample Output###

3.500

HINT###

【评分方式】

如果输出文件的答案与标准输出的差不超过0.001，则将获得该测试点上的分数，否则不得分。

【数据规模和约定】

20%的测试数据，满足：n≤10；

40%的测试数据，满足：n≤100；

85%的测试数据，满足：n≤2000；

100%的测试数据，满足：2≤n≤200000。

【说明】

树的高度：一棵有根树如果只包含一个根节点，那么它的高度为1。否则，它的高度为根节点的所有子树的高度的最大值加1。

对于树中任意的三个节点a , b , c ，如果a, b都是c的儿子，则a, b在BFS序中和DFS序中的相对前后位置是一致的，即要么a都在b的前方，要么a都在b的后方。

---

想法##

果然noi的题就是有水准啊666

%了各方题解，琢磨了3天才大概明白了这道题

首先将每个点重新编号使bfs为1 2 3 …，dfs对应一下，这样到后面会方便很多。

然后利用期望的线性性质，最终树的高度的期望值便为每个点对树的高度的贡献的期望值之和。

设c[i]为编号为i的点在dfs序中的位置，每个点的期望贡献值为p[i]

按照bfs的顺序考虑每个点（也就是重新编号后1~n的顺序）

有下面这几种情况：

1.c[i] < c[i-1]

那么i只能在i-1的下一行，故p[i]=1

2.c[i] > c[i-1]

那么i既有可能与i-1同行，也有可能在i-1下一行

可在i-1下一行的情况如下图所示：

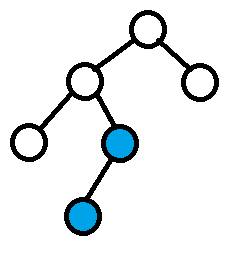
我们可以发现，蓝色的两个点必须满足在dfs序中相邻，且不会被其它点限制必须在同一行

会不会被两个点限制在同一行其实就是dfs序提供的信息了。

考虑dfs序中相邻的两点i,j（c[j]>c[i]），如果j>i，那么j要么是i的兄弟，要么是i的儿子

也就是说，i+1~j中所有点对树高度的贡献 \(\leq\) 1

刚刚上面所说的“被限制在同一行”其实就是这个东西。

对于每个限制，如果那一段区间内有确定的p[i]=1的点，那么其它点p[i']=0

都打上差分标记，最终没有被打标记且p[i]!=1的点就是既可作兄弟又可作儿子的点，p[i]=0.5

---

代码##

#include<cstdio>
#include<iostream>
#include<algorithm>

using namespace std;

const int N = 200005;

int n;
int a[N],b[N],c[N],p[N],sum[N],zz[N]; //zz差分 

int main()
{
	int x,s;
	scanf("%d",&n);
	for(int i=1;i<=n;i++) {
		scanf("%d",&x);
		p[x]=i;
	}
	for(int i=1;i<=n;i++){
		scanf("%d",&x);
		b[i]=i; a[p[x]]=i; c[i]=p[x];
	}

	if(n==1) { printf("1\n"); return 0; }

	p[1]=p[2]=1;
	sum[1]=1; sum[2]=2;
	for(int i=3;i<=n;i++){
		p[i]=0;
		if(c[i]<c[i-1]) p[i]=1;
		sum[i]=sum[i-1]+p[i];
	}
	for(int i=2;i<=n;i++)
		if(a[i]>a[i-1])
			if(sum[a[i]]-sum[a[i-1]]) zz[a[i-1]+1]++,zz[a[i]+1]--;

	double ans=0; s=0;
	for(int i=1;i<=n;i++){
		s+=zz[i];
		if(p[i]) ans+=1;
		else if(s==0) ans+=0.5;
	}
	printf("%.3lf\n%.3lf\n%.3lf\n",ans-0.001,ans,ans+0.001);  //bzoj神奇的输出格式

	return 0;
}