OpenCV实现图像变换（python）

一般对图像的变化操作有放大、缩小、旋转等，统称为几何变换，对一个图像的图像变换主要有两大步骤，一是实现空间坐标的转换，就是使图像从初始位置到终止位置的移动。二是使用一个插值的算法完成输出图像的每个像素的灰度值。其中主要的图像变换有：仿射变换、投影变换、极坐标变换。

仿射变换##

二维空间坐标的仿射变换公式：

\[\left(
\begin{matrix}
\overline{x} \\
\overline{y}
\end{matrix}
\right) =\left(
\begin{matrix}
a_{11} &&a_{12} \\
a_{21}&&a_{22}
\end{matrix}
\right) \left(
\begin{matrix}
x \\
y
\end{matrix}
\right) + \left(
\begin{matrix}
a_{13} \\
a_{23}
\end{matrix}
\right)
\]

在以下矩阵中：

\[\left(
\begin{matrix}
\overline{x} \\
\overline{y} \\
1
\end{matrix}
\right) =A \left(
\begin{matrix}
x \\
y \\
1
\end{matrix}
\right)
\]

矩阵A就是仿射矩阵，因为它最后一行为（0，0，1）

\[A=
\left(
\begin{matrix}
a_{11}&a_{12}&a_{13} \\
a_{21}&a_{22}&a_{23} \\
0&0&1
1
\end{matrix}
\right)
\]

平移

平移是最简单的仿射变换如将空间坐标（x,y)沿着x轴移动100，沿着y轴移动200。平移后的坐标为(x+100,y+200)。将这个过程一般化后，假设任意的空间坐标（x,y)先沿着x轴平移Px再沿着y轴平移Py。得到的坐标为（x+Px,y+Py)。用矩阵表示这个平移过程为：

\[\left(
\begin{matrix}
\overline{x} \\
\overline{y} \\
1
\end{matrix}
\right) =\left(
\begin{matrix}
1 &0&Px \\
0&1&Py \\
0&0&1
\end{matrix}
\right) \left(
\begin{matrix}
x \\
y \\
1
\end{matrix}
\right)
\]

对于Px和Py若大于0则表示沿着轴正向移动，若小于0则表示沿着轴负向移动。

放大缩小

在坐标轴中以原点为中心的放大与缩小S倍是指对其x轴方向的横坐标放缩成原坐标的横坐标距离中心点（0，0）的距离的S倍并对其y轴方向的横坐标放缩成原坐标的纵坐标距离原点的距离的S倍。其中若S大于1则表示增大，若小于1则表示缩小。放缩在矩阵中的表示为：

\[\left(
\begin{matrix}
\overline{x} \\
\overline{y} \\
1
\end{matrix}
\right) =\left(
\begin{matrix}
s_x&0&0 \\
0&s_y&0 \\
0&0&1
\end{matrix}
\right) \left(
\begin{matrix}
x \\
y \\
1
\end{matrix}
\right)
\]

坐标(x,y)在坐标轴中以任意一点的坐标(x0,y0)为中心在水平和垂直方向上放缩S倍，放缩后的坐标为$$ ( (x_0+S_x(x-x_0),y_0+S_y(y-y_0) )$$用矩阵可以表示为：

\[\left(
\begin{matrix}
\overline{x} \\
\overline{y} \\
1
\end{matrix}
\right) =\left(
\begin{matrix}
1 &0&X_0 \\
0&1&Y_0 \\
0&0&1
\end{matrix}
\right) \left(
\begin{matrix}
s_x&0&0 \\
0&s_y&0 \\
0&0&1
\end{matrix}
\right) \left(
\begin{matrix}
1 &0&-X_0 \\
0&1&-Y_0 \\
0&0&1
\end{matrix}
\right) \left(
\begin{matrix}
x \\
y \\
1
\end{matrix}
\right)
\]

坐标(x,y)绕原点顺时针旋转α(α>0)，cosΘ=x/p sinΘ=y/p.其中p代表（x,y)到中心点（0,0)的距离。则

cos(Θ+α)=cosΘcosα-sinΘsinα=(x/p)cosα -(y/p)sinα=Ex/p

sin(Θ+α)=sinΘcosα+cosΘsinα=(y/p)cosα -(y/p)sinα=Ey/p

化解以上公式，使用矩阵表示为：

\[\left(
\begin{matrix}
\overline{x} \\
\overline{y} \\
1
\end{matrix}
\right) =\left(
\begin{matrix}
cosα&-sinα&0 \\
sinα&cosα&0 \\
0&0&1
\end{matrix}
\right) \left(
\begin{matrix}
x \\
y \\
1
\end{matrix}
\right)
\]

放射矩阵的计算

如果已知坐标以及其放射变换后的矩阵，从而计算出变换后的坐标，就需要放射矩阵的计算，主要的实现方法有：方程法，矩阵法，插值算法。在OpenCV中有对应的实现函数，如使用方程法：cv2.getAffineTransform(src,dst) 该方法就是通过计算参数src到dst的对应仿射变换的矩阵，其中参数src和dst分别代表原坐标和变换后的坐标，并且均为3行2列的二维ndarray,数据必须为浮点型。实现代码：

import numpy as np

src=np.array([[0,0],[200,0],[0,200]],np.float32)
dst=np.array([[0,0],[100,0],[0,100]],np.float32)
A=cv2.getAffineTransform(src,dst)

print(A)

运行结果：



在矩阵法中，需要预先知道具体的变化步骤，比如先放大再平移还是先移动再放大

\[\left(
\begin{matrix}
\overline{x} \\
\overline{y} \\
1
\end{matrix}
\right) =\left(
\begin{matrix}
1 &0&X_0 \\
0&1&Y_0 \\
0&0&1
\end{matrix}
\right) \left(
\begin{matrix}
s_x&0&0 \\
0&s_y&0 \\
0&0&1
\end{matrix}
\right) \left(
\begin{matrix}
x \\
y \\
1
\end{matrix}
\right)
\]

以上的矩阵变换就是平移仿射矩阵乘以缩放仿射矩阵得到的而不是缩放仿射矩阵乘以平移仿射矩阵得到的，由于等式是由右向左运行，所以必须要知道变化顺序。矩阵的乘法并不是矩阵的点乘，再Numpy中乘法是通过dot函数实现的，关于Numpy语法可以参考我之前写的博文。我们通过一个实例来了解矩阵的乘法计算。

假设先对一矩阵等比例放大二倍，然后水平与垂直方向上分别平移100，计算该矩阵的算法如下：

import numpy as np

#先对矩阵进行放大
s=np.array([[2,0,0],[0,2,0],[0,0,1]])
#再对矩阵进行平移
t=np.array([[1,0,100],[0,1,100],[0,0,1]])
#矩阵相乘
A=np.dot(t,s)
print(A)

运行结果：



一定要注意传入dot参数的顺序。

下面介绍插值算法，我们可以将图像理解为一个二维的函数，行数为H，列数为W的图像矩阵I：Z=F(x,y), 0<=x<W,0<=y<H,x⊆N，y⊆N

矩阵的列号对应x坐标，垂直方向为y轴，行号对应y坐标，称该函数为图像函数。

利用已知的整数坐标处的函数值估算非整数坐标处的函数值的方法主要有：最近邻插值（就是从四个相邻整数坐标中找到一个最近的）输出的图像经过放大后会有锯齿状的外观。双线性插值法有两个变量的插值函数的线性插值扩展，其核心是在两个方向分别进行一次线性插值。待插点像素值取原图像中与其相邻的４个点像素值的水平、垂直两个方向上的线性内插，即根据待采样点与周围４个邻点的距离确定相应的权重，从而计算出待采样点的像素值。有的时候需要更高阶的插值函数，如三次样条插值、Lengendre中心函数和sin(axs）函数，高阶插值常用二维离散卷积运算来实现。后续博客会对二维离散卷积运算做详细的描述。

对于双线性插值法在这表一次形象化的描述：

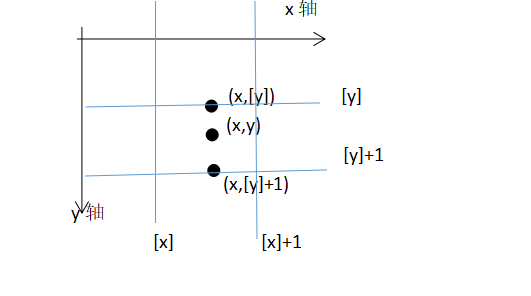
如图：先估计f1在（x,[y])处的函数值，再估计f1在(x,[y]+1)处的函数值，最后估计f1在（x,y)处的函数值

对于空间坐标变换和插值方法在已知的仿射变换矩阵上OpenV提供了warpAffine(src,M,dsize[,flags[,borderMode[,borderValue ]]])函数

参数	释义
src	图像矩阵
M	2行3列的仿射变换矩阵
dsize	一个二元元组，输出图像的大小
flags	插值法：INTE_NEAREST、INTE_LINEAR（默认）等
borderMode	填充模式，如：BORDER_CONSTANT等
borderValue	当borderMode=BORDER_CONSTANT时的填充值

下面使用python实现图像的几何变换：

import numpy as np
import cv2
import sys
import math

img=cv2.imread('yun.jpg',cv2.IMREAD_GRAYSCALE)
cv2.imwrite('yun.jpg',img)
#原图的宽高
h,w=img.shape[:2]
#仿射变换矩阵 缩小2倍
A1=np.array([[0.5,0,0],[0,0.5,0]],np.float32)
A2=cv2.warpAffine(img,A1,(w,h),borderValue=126)
#缩小后平移
B1=np.array([[0.5,0,w/4],[0,0.5,h/4]],np.float32)
B2=cv2.warpAffine(img,B1,(w,h),borderValue=126)
#使图像旋转
C1=cv2.getRotationMatrix2D((w/2.0,h/2.0),30,1)
C2=cv2.warpAffine(img,C1,(w,h),borderValue=126)

cv2.imshow('img',img)
cv2.imshow('A2',A2)
cv2.imshow('B2',B2)
cv2.imshow('C2',C2)
cv2.waitKey(0)
cv2.destroyAllWindows()

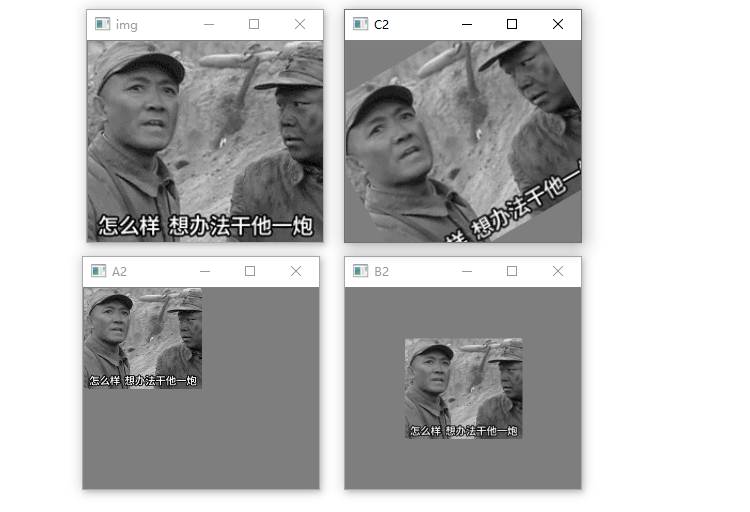
运行效果

参考文献：

[1]ROBERT G.KEYS.Cubic Convolution Interpolation for Digital Image Processing.IEEE TRANSACTIONS ON ACOUSTICS.SPEECH,AND SIGNAL PROCESSING,1981

[1]R. Hartley and A. Zisserman, “Multiple View Geometry in Computer Vision,” 2-nd edition, Cambridge University Press, 2004.

今天就先写到这吧！投影变换和极坐标变换后续再写