数学算法（一）：快速求斐波那契数第n项通过黄金分割率公式

有一个固定的数学公式= =，不知道的话显然没法应用

首先黄金分割率接近于这个公式，

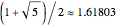
(以下为黄金分割率与斐波那契的关系，可跳过)

通过斐波那契数列公式

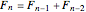
两边同时除以

得：

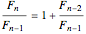（1）

注意后一项比前一项接近于黄金分割率

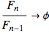（2）

那么前一项比后一项则为1/黄金分割率（备注：其实有这么一个规律0.618/1=1/1.618=1.618/2.618=0.618）

（3）

那么（2）（3）带入（1）可得

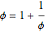
可以求得黄金分割率的根为

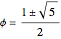
对于广义的斐波那契数列：

一般项可以表示为：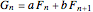

因此：

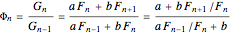
当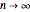 

这个函数趋向于

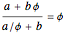
开始代码

a(n)为斐波那契数第n项，Binet 公式（推导过程见下最下方）

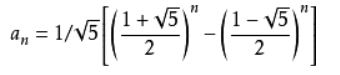
O(1)复杂度

Python

def fib(self, N):
　　golden_ratio = (1 + 5 ** 0.5) / 2
　　return int((golden_ratio ** N + 1) / 5 ** 0.5)

参考：

斐波那契数列与黄金分割率的关系：https://demonstrations.wolfram.com/GeneralizedFibonacciSequenceAndTheGoldenRatio/

Binet公式推导：https://www.sohu.com/a/284819172_614593