第三十三篇 玩转数据结构——红黑树（Read Black Tree）

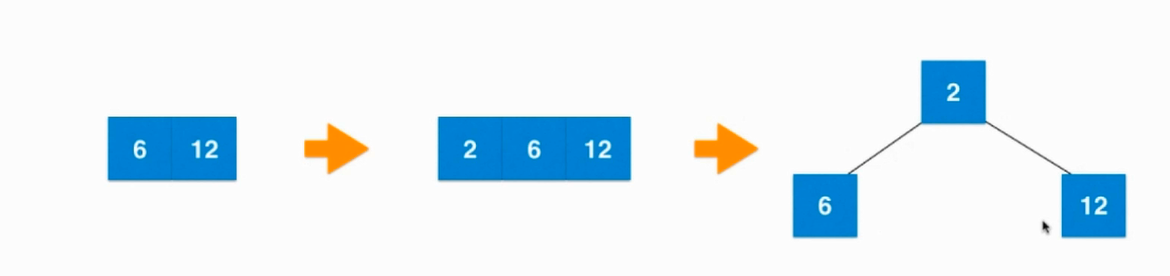
1.. 图解2-3树维持绝对平衡的原理：

• 
• 
• 
• 

2.. 红黑树与2-3树是等价的

• 
• 

3.. 红黑树的特点

• 

• 简要概括如下：
• 所有节点非黑即红；根节点为黑；NULL节点为黑；红节点孩子为黑；黑平衡

4.. 实现红黑树的业务逻辑

• import java.util.ArrayList;
  
  public class RBTree<K extends Comparable<K>, V> {
  
      private static final boolean RED = true;
      private static final boolean BLACK = false;
  
      private class Node{
          public K key;
          public V value;
          public Node left, right;
          public boolean color;
  
          public Node(K key, V value){
              this.key = key;
              this.value = value;
              left = null;
              right = null;
              color = RED;
          }
      }
  
      private Node root;
      private int size;
  
      public RBTree(){
          root = null;
          size = 0;
      }
  
      public int getSize(){
          return size;
      }
  
      public boolean isEmpty(){
          return size == 0;
      }
  
      // 判断节点node的颜色
      private boolean isRed(Node node){
          if(node == null)
              return BLACK;
          return node.color;
      }
  
      //   node                     x
      //  /   \     左旋转         /  \
      // T1   x   --------->   node   T3
      //     / \              /   \
      //    T2 T3            T1   T2
      private Node leftRotate(Node node){
  
          Node x = node.right;
  
          // 左旋转
          node.right = x.left;
          x.left = node;
  
          x.color = node.color;
          node.color = RED;
  
          return x;
      }
  
      //     node                   x
      //    /   \     右旋转       /  \
      //   x    T2   ------->   y   node
      //  / \                       /  \
      // y  T1                     T1  T2
      private Node rightRotate(Node node){
  
          Node x = node.left;
  
          // 右旋转
          node.left = x.right;
          x.right = node;
  
          x.color = node.color;
          node.color = RED;
  
          return x;
      }
  
      // 颜色翻转
      private void flipColors(Node node){
  
          node.color = RED;
          node.left.color = BLACK;
          node.right.color = BLACK;
      }
  
      // 向红黑树中添加新的元素(key, value)
      public void add(K key, V value){
          root = add(root, key, value);
          root.color = BLACK; // 最终根节点为黑色节点
      }
  
      // 向以node为根的红黑树中插入元素(key, value)，递归算法
      // 返回插入新节点后红黑树的根
      private Node add(Node node, K key, V value){
  
          if(node == null){
              size ++;
              return new Node(key, value); // 默认插入红色节点
          }
  
          if(key.compareTo(node.key) < 0)
              node.left = add(node.left, key, value);
          else if(key.compareTo(node.key) > 0)
              node.right = add(node.right, key, value);
          else // key.compareTo(node.key) == 0
              node.value = value;
  
          if (isRed(node.right) && !isRed(node.left))
              node = leftRotate(node);
  
          if (isRed(node.left) && isRed(node.left.left))
              node = rightRotate(node);
  
          if (isRed(node.left) && isRed(node.right))
              flipColors(node);
  
          return node;
      }
  
      // 返回以node为根节点的二分搜索树中，key所在的节点
      private Node getNode(Node node, K key){
  
          if(node == null)
              return null;
  
          if(key.equals(node.key))
              return node;
          else if(key.compareTo(node.key) < 0)
              return getNode(node.left, key);
          else // if(key.compareTo(node.key) > 0)
              return getNode(node.right, key);
      }
  
      public boolean contains(K key){
          return getNode(root, key) != null;
      }
  
      public V get(K key){
  
          Node node = getNode(root, key);
          return node == null ? null : node.value;
      }
  
      public void set(K key, V newValue){
          Node node = getNode(root, key);
          if(node == null)
              throw new IllegalArgumentException(key + " doesn't exist!");
  
          node.value = newValue;
      }
  
      // 返回以node为根的二分搜索树的最小值所在的节点
      private Node minimum(Node node){
          if(node.left == null)
              return node;
          return minimum(node.left);
      }
  
      // 删除掉以node为根的二分搜索树中的最小节点
      // 返回删除节点后新的二分搜索树的根
      private Node removeMin(Node node){
  
          if(node.left == null){
              Node rightNode = node.right;
              node.right = null;
              size --;
              return rightNode;
          }
  
          node.left = removeMin(node.left);
          return node;
      }
  
      // 从二分搜索树中删除键为key的节点
      public V remove(K key){
  
          Node node = getNode(root, key);
          if(node != null){
              root = remove(root, key);
              return node.value;
          }
          return null;
      }
  
      private Node remove(Node node, K key){
  
          if( node == null )
              return null;
  
          if( key.compareTo(node.key) < 0 ){
              node.left = remove(node.left , key);
              return node;
          }
          else if(key.compareTo(node.key) > 0 ){
              node.right = remove(node.right, key);
              return node;
          }
          else{   // key.compareTo(node.key) == 0
  
              // 待删除节点左子树为空的情况
              if(node.left == null){
                  Node rightNode = node.right;
                  node.right = null;
                  size --;
                  return rightNode;
              }
  
              // 待删除节点右子树为空的情况
              if(node.right == null){
                  Node leftNode = node.left;
                  node.left = null;
                  size --;
                  return leftNode;
              }
  
              // 待删除节点左右子树均不为空的情况
  
              // 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
              // 用这个节点顶替待删除节点的位置
              Node successor = minimum(node.right);
              successor.right = removeMin(node.right);
              successor.left = node.left;
  
              node.left = node.right = null;
  
              return successor;
          }
      }
  
      public static void main(String[] args){
  
          System.out.println("Pride and Prejudice");
  
          ArrayList<String> words = new ArrayList<>();
          if(FileOperation.readFile("pride-and-prejudice.txt", words)) {
              System.out.println("Total words: " + words.size());
  
              RBTree<String, Integer> map = new RBTree<>();
              for (String word : words) {
                  if (map.contains(word))
                      map.set(word, map.get(word) + 1);
                  else
                      map.add(word, 1);
              }
  
              System.out.println("Total different words: " + map.getSize());
              System.out.println("Frequency of PRIDE: " + map.get("pride"));
              System.out.println("Frequency of PREJUDICE: " + map.get("prejudice"));
          }
  
          System.out.println();
      }
  }

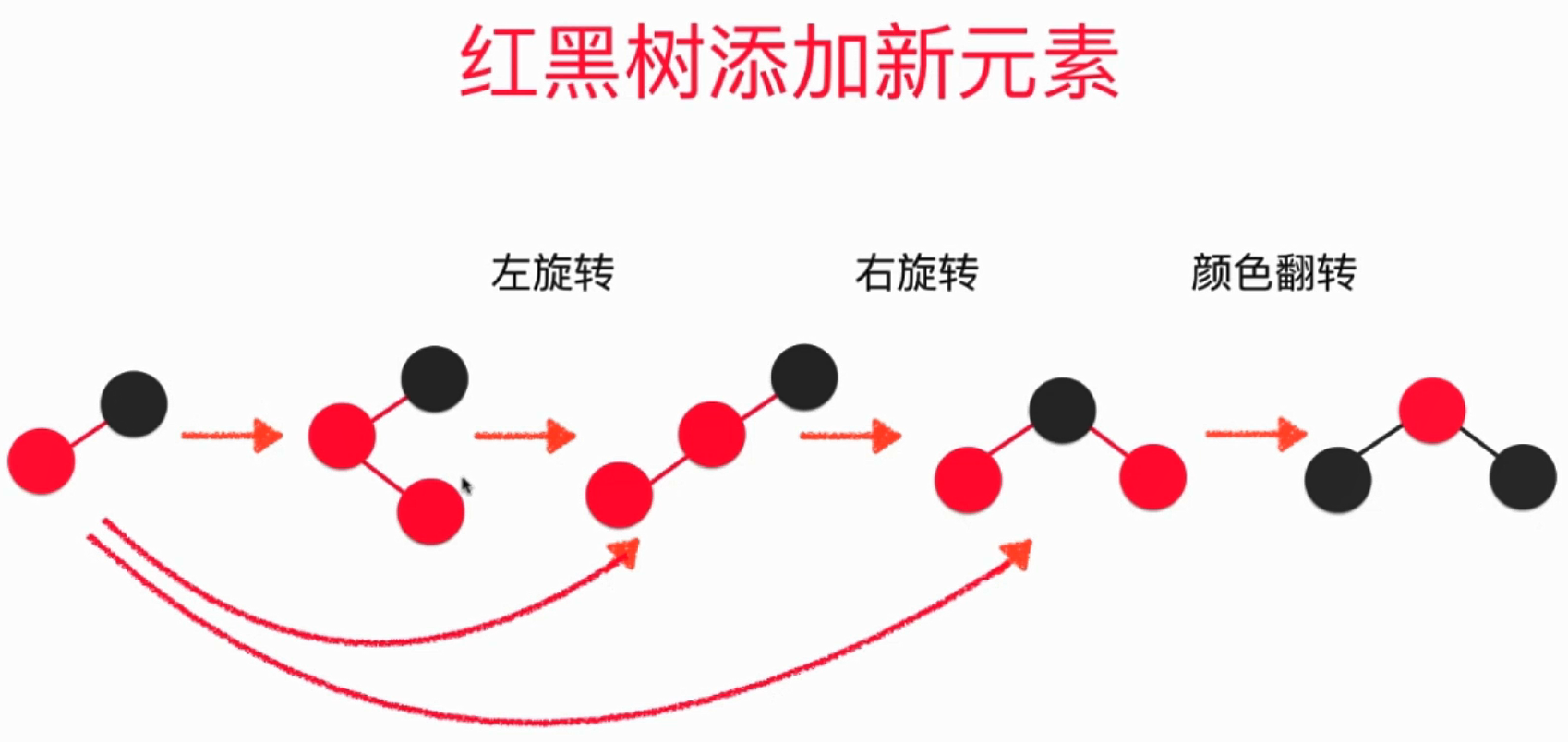
5.. 向红黑树中添加新元素之后需要进行维护的过程示意图

•