BZOJ 2119 股市的预测（后缀数组）

首先要差分+离散化。

然后就是求形如ABA的串有多少，其中B的长度确定为k。

我们用到了设置关键点的思想。我们枚举A的长度L。然后在\(1,1+L,1+L*2,1+L*3。。。\)设置关键点。然后我们枚举这些关键点，试图求出跨过这个关键点的长度为L的在B左边的A有多少个。

可以证明这样可以做到不重不漏，因为A的长度为L至少跨过一个关键点。

然后这个点的贡献就怎么算？我们先处理出后缀数组。然后对枚举的关键点i和i+L+k求LCP和LCS。贡献就是(min(LCP,L)+min(LCS,L)-1)-L+1。为什么是这个呢？

当K=4，L=3时，如图

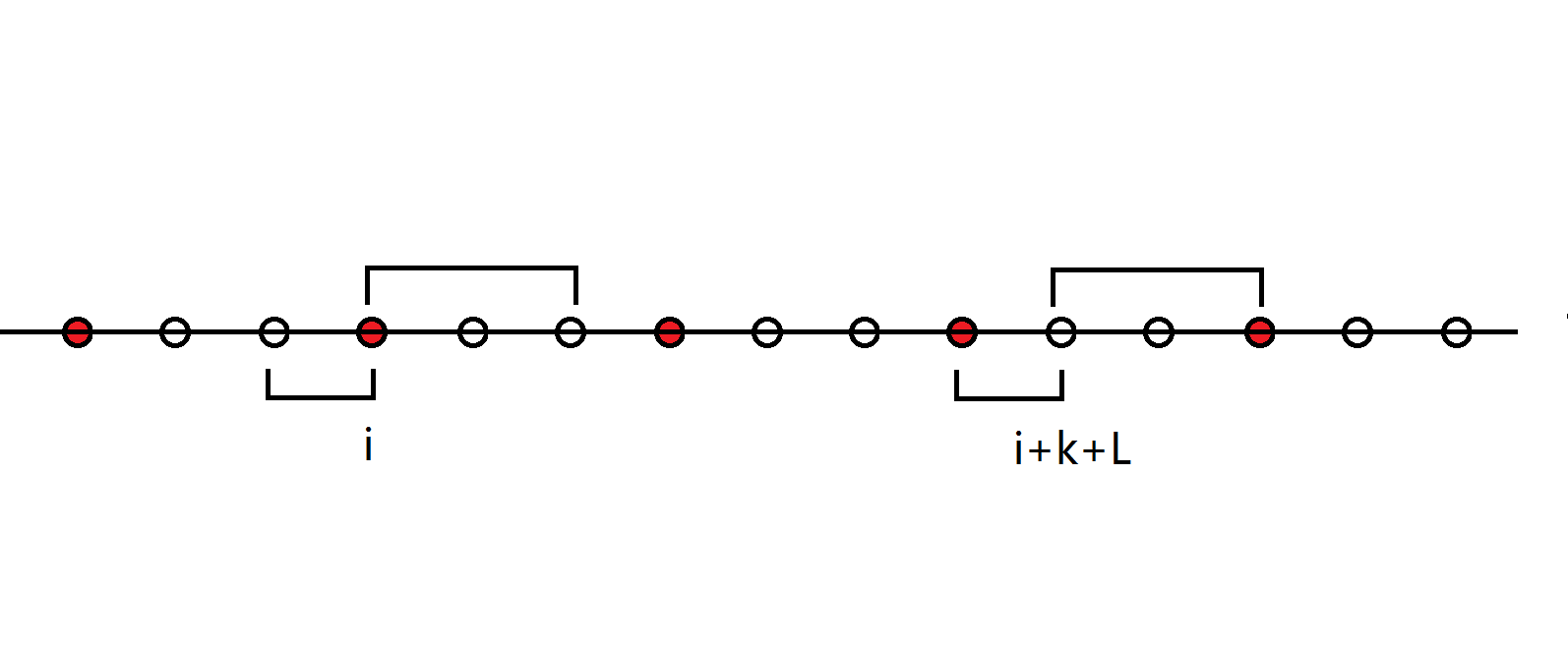实际上我们是确定了左边A的区间就是\([i-LCP+1,i+LCS-1]\)，然后A的个数就是长度-L+1，因为考虑到不跨过关键点要对L取min。为了排除负数贡献，最后这个贡献还要对0取max。

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
const int N=100100;
int ans,n,a[N],b[N],k;
struct SA{
	int c[N],x[N],y[N],m,sa[N],rk[N],height[N],mn[N][20],s[N];
	void get_sa(){
		for(int i=1;i<=m;i++)c[i]=0;
		for(int i=1;i<=n;i++)c[x[i]=s[i]]++;
		for(int i=1;i<=m;i++)c[i]+=c[i-1];
		for(int i=n;i>=1;i--)sa[c[x[i]]--]=i;
		for(int k=1;k<=n;k<<=1){
			int num=0;
			for(int i=n-k+1;i<=n;i++)y[++num]=i;
			for(int i=1;i<=n;i++)if(sa[i]>k)y[++num]=sa[i]-k;
			for(int i=1;i<=m;i++)c[i]=0;
			for(int i=1;i<=n;i++)c[x[i]]++;
			for(int i=1;i<=m;i++)c[i]+=c[i-1];
			for(int i=n;i>=1;i--)sa[c[x[y[i]]]--]=y[i],y[i]=0;
			for(int i=1;i<=n;i++)swap(x[i],y[i]);
			x[sa[1]]=1;num=1;
			for(int i=2;i<=n;i++)
				x[sa[i]]=(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])?num:++num;
			if(n==num)break;
			m=num;
		}
	}
	void get_height(){
		int k=0;
		for(int i=1;i<=n;i++)rk[sa[i]]=i;
		for(int i=1;i<=n;i++){
			if(rk[i]==1)continue;
			if(k)k--;
			int j=sa[rk[i]-1];
			while(i+k<=n&&j+k<=n&&s[i+k]==s[j+k])k++;
			height[rk[i]]=k;
		}
	}
	void pre_work(){
		for(int i=1;i<=n;i++)mn[i][0]=height[i];
		int len=log2(n);
		for(int j=1;j<=len;j++)
			for(int i=1;i+(1<<j)-1<=n;i++)
				mn[i][j]=min(mn[i][j-1],mn[i+(1<<j-1)][j-1]);
	}
	int getlcp(int l,int r){
		if(l>r)swap(l,r);
		l++;
		int len=log2(r-l+1);
		return min(mn[l][len],mn[r-(1<<len)+1][len]);
	}
}A,B;
int read(){
	int sum=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){sum=sum*10+ch-'0';ch=getchar();}
	return sum*f;
}
int main(){
	n=read();k=read();
	for(int i=1;i<=n;i++)a[i]=read();
	for(int i=1;i<n;i++)a[i]=a[i+1]-a[i],b[i]=a[i];
	n--;
	sort(b+1,b+1+n);
	int tot=unique(b+1,b+1+n)-b-1;
	for(int i=1;i<=n;i++)a[i]=lower_bound(b+1,b+1+tot,a[i])-b;
	for(int i=1;i<=n;i++)A.s[i]=a[i],B.s[i]=a[n-i+1];
	A.m=B.m=51000;
	A.get_sa();A.get_height();A.pre_work();
	B.get_sa();B.get_height();B.pre_work();
	for(int i=1;i<=n;i++)
		for(int j=1;j+i+k<=n;j+=i)
			ans+=max(min(i,A.getlcp(A.rk[j],A.rk[j+i+k]))+min(i,B.getlcp(B.rk[n-j+1],B.rk[n-(j+i+k)+1]))-1,i-1)-(i-1);
	printf("%d",ans);
	return 0;
}