php实现变态跳台阶（记忆化递归）

php实现变态跳台阶（记忆化递归）

一、总结

1、本题思路（分类讨论思路，注意初始值和边界值）：第一步如果1，那剩下的就是jumpFloorII($number-1)(下面jumpFloorII以j表示)，第一步如果2，那剩下的就是j($number-2)，...，以此类推

所以j(n)=j(n-1)+j(n-2)+...+j(0)，其实j(n)就是2的n次方

二、php实现变态跳台阶

一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

三、代码

牛客网ac代码一：

 <?php

 $arr = array(1,1,2,4);//记忆化递归数组  1、$arr[0]=1而不是0
 for($i=4;$i<500;$i++) $arr[$i]=-1;
 function jumpFloorII($number)
 {
     global $arr;
     if($arr[$number]!=-1) return $arr[$number]; //2、这里的$arr忘记接[$number]
     $ans=0;
     for($i=1;$i<=$number;$i++){
         $arr[$number-$i]=$arr[$number-$i]!=-1?$arr[$number-$i]:jumpFloorII($number-$i); //3、这里的变量i漏掉了$符号
         $ans+=$arr[$number-$i];
     }
     return $arr[$number]=$ans;
 }

代码二：

 //变态跳台阶
 private $arr = array();//记忆化递归数组
 public function jumpFloorII($number)
 {
     global $arr;
     if($arr[$number]!=-1) return $arr[$number];
     $ans=0;
     for($i=1;$i<=$number;$i++){
         $arr[$number-$i]=$arr[$number-$i]!=-1?$arr[$number-$i]:$this->jumpFloorII($number-$i);
         $ans+=$arr[$number-$i];
     }
     return $arr[$number]=$ans;
 }
 public function jumpFloorIIDemo(){
     global $arr;
     for($i=0;$i<500;$i++) $arr[$i]=-1;
     $arr[0]=1;
     $arr[1]=1;
     $arr[2]=2;
     $arr[3]=4;
     echo($this->jumpFloorII(30));
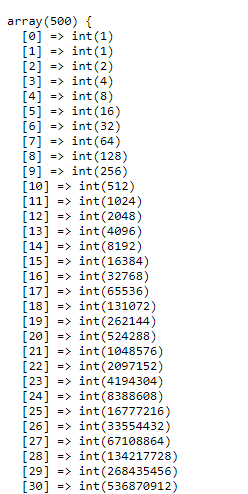
     dump($arr);die;
 }