[luogu]P4365[九省联考]秘密袭击coat（非官方正解）

题目背景

警告：滥用本题评测者将被封号

We could have had it all. . . . . .

我们本该，拥有一切

Counting on a tree. . . . . .

何至于此，数数树上

Counting on a Tree（CoaT）即是本题的英文名称。

题目描述

Access Globe 最近正在玩一款战略游戏。在游戏中，他操控的角色是一名C 国士 兵。他的任务就是服从指挥官的指令参加战斗，并在战斗中取胜。

C 国即将向D 国发动一场秘密袭击。作战计划是这样的：选择D 国的s 个城市， 派出C 国战绩最高的s 个士兵分别秘密潜入这些城市。每个城市都有一个危险程度d_idi​，

C 国指挥官会派遣战绩最高的士兵潜入所选择的城市中危险程度最高的城市，派遣战绩第二高的士兵潜入所选择的城市中危险程度次高的城市，以此类推（即派遣战绩第i高的士兵潜入所选择城市中危险程度第i 高的城市）。D 国有n 个城市，n - 1 条双向道路连接着这些城市，使得这些城市两两之间都可以互相到达。为了任务执行顺利，C 国选出的s 个城市中，任意两个所选的城市，都可以不经过未被选择的城市互相到达。

Access Globe 操控的士兵的战绩是第k 高，他希望能估计出最终自己潜入的城市的 危险程度。Access Globe 假设C 国是以等概率选出任意满足条件的城市集合S ，他希望你帮他求出所有可能的城市集合中，Access Globe 操控的士兵潜入城市的危险程度之和。如果选择的城市不足k 个，那么Access Globe 不会被派出，这种情况下危险程度为0。

当然，你并不想帮他解决这个问题，你也不打算告诉他这个值除以998 244 353 的 余数，你只打算告诉他这个值除以64,123 的余数。

输入输出格式

输入格式：

从文件coat.in 中读入数据。

第1 行包含3 个整数n、k、W，表示D 国城市的个数、Access Globe 所操控士兵 潜入的城市战绩排名以及D 国的所有城市中最大的危险程度；

第2 行包含n 个1 到W 之间的整数d_1d1​; d_2d2​; ... d_ndn​，表示每个城市的危险程度；

第3 行到第n + 1 行，每行两个整数x_ixi​; y_iyi​，表示D 国存在一条连接城市x_ixi​ 和城市y_iyi​ 的双向道路。

输出格式：

输出到文件coat.out 中。 输出一个整数，表示所有可行的城市集合中，Access Globe 操控的士兵潜入城市的危险程度之和除以64,123 的余数。

输入输出样例

输入样例#1： 复制

5 3 3

2 1 1 2 3

1 2

2 3

1 4

1 5

输出样例#1： 复制

11

输入样例#2： 复制

10 2 3

2 1 1 3 1 2 3 3 1 3

1 2

2 3

2 4

2 5

2 6

5 7

1 8

8 9

1 10

输出样例#2： 复制

435

说明

D 国地图如下，其中危险程度为d 的城市的形状是(d + 3) 边形。

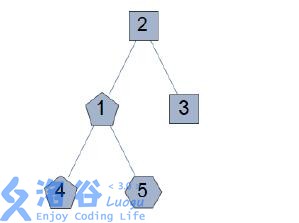
以下是所有符合条件且选择的城市不少于3 个的方案：

• 选择城市1、2、3，Access Globe 的士兵潜入的城市危险程度为1；

• 选择城市1、2、3、4，Access Globe 的士兵潜入的城市危险程度为1；

• 选择城市1、2、3、5，Access Globe 的士兵潜入的城市危险程度为1；

• 选择城市1、2、3、4、5，Access Globe 的士兵潜入的城市危险程度为2；

• 选择城市1、2、4，Access Globe 的士兵潜入的城市危险程度为1；

• 选择城市1、2、5，Access Globe 的士兵潜入的城市危险程度为1；

• 选择城市1、2、4、5，Access Globe 的士兵潜入的城市危险程度为2；

• 选择城市1、4、5，Access Globe 的士兵潜入的城市危险程度为2；而在选择的 城市少于3 时，Access Globe 的士兵潜入的城市危险程度均为0；

所以你应该输出(1 + 1 + 1 + 2 + 1 + 1 + 2 + 2) mod 64 123 = 11。

题解

这道题教会我们。

暴力是一定要打的．信仰是一定要有的。

万一A了呢？

因为本题正解涉及的算法过多且复杂。

所以暴力效率似乎>>正解。就像一些树套树的题目被分块水掉一样。

现在来讲暴力。

设f[i][j]表示第i个节点为根的子树,选了j个比当前预想的值大的方案。

那么转移方程为

\(if(ch[u]>ch[now])f[v][j+1]+=f[u][j];\)

\(if(ch[u]<ch[now])f[v][j]+=f[u][j];\)

但是相同的值呢？

我们把序号进行比较，这样我们就不会重复计算了。

对于每一个子树处理完之后，我们要加上它的值

\(f[u][i]+=f[v][i]\)

为什么？因为只要向下选了就是一种方案。

我们枚举一重循坏枚举当前哪个点要选

便利一遍树，对于每一个节点枚举k值。

就可以了。是的，w并没卵用。暴力出奇迹！！

Code

#include<cstdio>
#include<cstring>
#include<cmath>
#include<iostream>
#include<algorithm>
using namespace std;
const int mod=64123;
const int N=1675;
int n,k,w,ch[N],now,ans;
int f[N][N],num,head[N];
struct node{
	int to,nex;
}e[N<<1];
int read(){
	int x=0,w=1;char ch=getchar();
	while(ch>'9'||ch<'0'){if(ch=='-')w=-1;ch=getchar();}
	while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
	return x*w;
}

void add(int from,int to){
	num++;
	e[num].to=to;
	e[num].nex=head[from];
	head[from]=num;
}

void dfs(int x,int ff){
	for(int i=head[x];i;i=e[i].nex){
		int v=e[i].to;if(v==ff)continue;
		if((ch[v]>ch[now])||(ch[v]==ch[now]&&v>now))
			for(int j=1;j<k;j++)f[v][j+1]+=f[x][j],f[v][j+1]%=mod;
		else for(int j=1;j<=k;j++)f[v][j]+=f[x][j],f[v][j]%=mod;
		dfs(v,x);for(int j=1;j<=k;j++)f[x][j]+=f[v][j],f[x][j]%=mod;
	}
}

int main(){
	n=read();k=read();w=read();
	for(int i=1;i<=n;i++)ch[i]=read();
	for(int i=1;i<n;i++){
		int x=read(),y=read();
		add(x,y);add(y,x);
	}
	for(int i=1;i<=n;i++){
		now=i;memset(f,0,sizeof(f));
		int tot=0;
		for(int j=1;j<=n;j++)
			if((ch[j]>ch[now])||(ch[j]==ch[now]&&j>now))tot++;
		if(tot<k-1)continue;
		f[i][1]=1;dfs(i,i);	ans+=f[i][k]*ch[i];ans%=mod;
	}printf("%d\n",ans%mod);
	return 0;
}