hdu-2685 I won't tell you this is about number theory---gcd和快速幂的性质

题目链接：

http://acm.hdu.edu.cn/showproblem.php?pid=2685

题目大意：

求gcd(a^m-1,aⁿ-1)%k

解题思路：

对于a^m-1 = (a - 1) * (1 + a + a² + ... + a^m-1)

所以最开始的gcd就为a-1

对于两个1 + a + a² + ... + a^m-1和1 + a + a² + ... + a^n-1来说，可以找出gcd(m, n)那么久就可以提出gcd

比如：

1 + a + a² + a³

1 + a + a² + ... + a⁵

这两个可以写成（1+a）*（1 + a²） 和（1+a）*（1 + a²+ a⁴）

就提出公因式(1 + a)

这里公因式如何确定呢？

就是从0一直加到m和n的gcd-1次方，这样的话m和n才可以分解成多个从0---gcd-1的幂之和

所以，gcd(a^m-1,aⁿ-1) = （a-1）*（1 + a + a² + a³ + ... + a^g-1） = a^g - 1

上式中g等于gcd(m, n)

也就是这个式子：

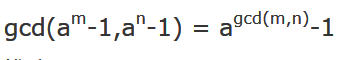
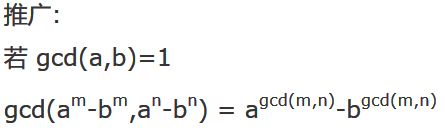
 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 int pow(int a, int b, int m)
 {
     int ans = ;
     a %= m;
     while(b)
     {
         if(b & )ans = ans * a % m;
         a *= a;
         a %= m;
         b /= ;
     }
     return ans;
 }
 int main()
 {
     int T, a, m, n, k, g;
     cin >> T;
     while(T--)
     {
         cin >> a >> m >> n >> k;
         g = __gcd(m, n);
         int ans = (pow(a, g, k) - ) % k;
         ans = (ans + k) % k;
         cout<<ans<<endl;
     }
     return ;
 }