URAL 1519 Formula 1(插头DP,入门题)
Description
Background
Problem
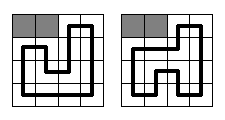
Input
Output
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
typedef long long LL; const int MAXH = ;
const int SIZEH = ; struct hash_map {
int head[SIZEH];
int next[MAXH], state[MAXH];
LL value[MAXH];
int size; void init() {
memset(head, -, sizeof(head));
size = ;
} void insert(int st, LL tv) {
int h = st % SIZEH;
for(int i = head[h]; ~i; i = next[i]) {
if(state[i] == st) {
value[i] += tv;
return ;
}
}
value[size] = tv; state[size] = st;
next[size] = head[h]; head[h] = size++;
}
} hashmap[]; hash_map *cur, *last;
int acc[] = {, -, , }; int n, m, en, em;
char mat[][]; int getB(int state, int i) {
i <<= ;
return (state >> i) & ;
} int getLB(int state, int i) {
int ret = i, cnt = ;
while(cnt) cnt += acc[getB(state, --ret)];
return ret;
} int getRB(int state, int i) {
int ret = i, cnt = -;
while(cnt) cnt += acc[getB(state, ++ret)];
return ret;
} void setB(int &state, int i, int tv) {
i <<= ;
state = (state & ~( << i)) | (tv << i);
} void update(int x, int y, int state, LL tv) {
int left = getB(state, y);
int up = getB(state, y + );
if(mat[x][y] == '*') {
if(left == && up == ) cur->insert(state, tv);
return ;
}
if(left == && up == ) {
if(x == n - || y == m - ) return ;
int newState = state;
setB(newState, y, );
setB(newState, y + , );
cur->insert(newState, tv);
} else if(left == || up == ) {
if(x < n - ) {
int newState = state;
setB(newState, y, up + left);
setB(newState, y + , );
cur->insert(newState, tv);
}
if(y < m - ) {
int newState = state;
setB(newState, y, );
setB(newState, y + , up + left);
cur->insert(newState, tv);
}
} else {
int newState = state;
setB(newState, y, );
setB(newState, y + , );
if(left == && up == ) setB(newState, getRB(state, y + ), );
if(left == && up == && !(x == en && y == em)) return ;
if(left == && up == ) setB(newState, getLB(state, y), );
cur->insert(newState, tv);
}
} void findend() {
for(en = n - ; en >= ; --en)
for(em = m - ; em >= ; --em) if(mat[en][em] == '.') return ;
} LL solve() {
findend();
cur = hashmap, last = hashmap + ;
last->init();
last->insert(, );
for(int i = ; i < n; ++i) {
int sz = last->size;
for(int k = ; k < sz; ++k) last->state[k] <<= ;
for(int j = ; j < m; ++j) {
cur->init();
sz = last->size;
for(int k = ; k < sz; ++k)
update(i, j, last->state[k], last->value[k]);
swap(cur, last);
}
}
return last->size ? last->value[] : ;
} int main() {
scanf("%d%d", &n, &m);
for(int i = ; i < n; ++i) scanf("%s", mat[i]);
cout<<solve()<<endl;
}
URAL 1519 Formula 1(插头DP,入门题)的更多相关文章
- bzoj1814 Ural 1519 Formula 1(插头dp模板题)
1814: Ural 1519 Formula 1 Time Limit: 1 Sec Memory Limit: 64 MBSubmit: 924 Solved: 351[Submit][Sta ...
- bzoj 1814: Ural 1519 Formula 1 插头dp经典题
用的括号序列,听说比较快. 然并不会预处理,只会每回暴力找匹配的括号. #include<iostream> #include<cstdio> #include<cstr ...
- 【BZOJ1814】Ural 1519 Formula 1 插头DP
[BZOJ1814]Ural 1519 Formula 1 题意:一个 m * n 的棋盘,有的格子存在障碍,求经过所有非障碍格子的哈密顿回路个数.(n,m<=12) 题解:插头DP板子题,刷板 ...
- bzoj 1814 Ural 1519 Formula 1 插头DP
1814: Ural 1519 Formula 1 Time Limit: 1 Sec Memory Limit: 64 MBSubmit: 942 Solved: 356[Submit][Sta ...
- Ural 1519 Formula 1 插头DP
这是一道经典的插头DP单回路模板题. 用最小表示法来记录连通性,由于二进制的速度,考虑使用8进制. 1.当同时存在左.上插头的时候,需要判断两插头所在连通块是否相同,若相同,只能在最后一个非障碍点相连 ...
- bzoj 1814 Ural 1519 Formula 1 ——插头DP
题目:https://www.lydsy.com/JudgeOnline/problem.php?id=1814 普通的插头 DP .但是调了很久.注意如果合并两个 1 的话,不是 “把向右第一个 2 ...
- BZOJ1814: Ural 1519 Formula 1(插头Dp)
Description Regardless of the fact, that Vologda could not get rights to hold the Winter Olympic gam ...
- 【Ural】1519. Formula 1 插头DP
[题目]1519. Formula 1 [题意]给定n*m个方格图,有一些障碍格,求非障碍格的哈密顿回路数量.n,m<=12. [算法]插头DP [题解]<基于连通性状态压缩的动态规划问题 ...
- [URAL1519] Formula 1 [插头dp入门]
题面: 传送门 思路: 插头dp基础教程 先理解一下题意:实际上就是要你求这个棋盘中的哈密顿回路个数,障碍不能走 看到这个数据范围,还有回路处理,就想到使用插头dp来做了 观察一下发现,这道题因为都是 ...
- 【BZOJ1814】Ural 1519 Formula 1 (插头dp)
[BZOJ1814]Ural 1519 Formula 1 (插头dp) 题面 BZOJ Vjudge 题解 戳这里 上面那个链接里面写的非常好啦. 然后说几个点吧. 首先是关于为什么只需要考虑三进制 ...
随机推荐
- LeetCode 中级 -二叉树的层次遍历(102)
题目描述: 给定一个二叉树,返回其按层次遍历的节点值. (即逐层地,从左到右访问所有节点). 例如:给定二叉树: [3,9,20,null,null,15,7], 3 / \ 9 20 / \ 15 ...
- Oracle批量删除表格数据
在开发阶段往Oracle数据库中多个表格中导入了许多测试数据,倘若一张张表执行"truncate table tablename"语句显得十分繁琐.在PL/SQL中可以用代码进行批 ...
- JavaScript中Array的正确使用方式
在 JavaScript 中正确使用地使用 Array 的方法如下: 用 Array.includes 代替 Array.indexOf “如果你要在数组中查找元素,请使用 Array.indexOf ...
- Jquery拼图
Jquery代码 <script> $(function () { $("td").click(function () { var img = $(this).prop ...
- Angular.js进阶
1.常用指令 <!DOCTYPE html> <html> <head lang="en"> <meta charset="UT ...
- 01-http简介-四层 七层 三次握手
HTTP简介.请求方法与响应状态码 接下来想系统的回顾一下TCP/IP协议族的相关东西,当然这些东西大部分是在大学的时候学过的,但是那句话,基础的东西还是要不时的回顾回顾的.接下来的几篇博客都是关于T ...
- React组件的使用
一.index.js 文件[基本配置] //react语法塘 import React from 'react'; //reactDom用来操作虚拟DOM import ReactDom from ...
- MapReduce之Map Join
一 介绍 之所以存在Reduce Join,是因为在map阶段不能获取所有需要的join字段,即:同一个key对应的字段可能位于不同map中.Reduce side join是非常低效的,因为shuf ...
- 【一】调通单机版的thrift-python版本
开发步骤说明 [任务1]调通单机版的thrift-python版本 [任务1]调通单机版的thrift-python版本 安装thrift 创建thrift模块文件并编译 开发python版的clie ...
- 树莓派3B+学习笔记:3、启用root账户
1.打开终端,输入 sudo passwd root 输入两次密码后设置root账户密码: 2.输入 sudo passwd --unlock root 解锁root账户: 3.点击主菜单的“Shut ...
