[JXOI2017]颜色 线段树扫描线 + 单调栈

～～～题面～～～

题解：

　　首先题目要求删除一些颜色，换个说法就是要求保留一些颜色，那么观察到，如果我们设ll[i]和rr[i]分别表示颜色i出现的最左边的那个点和最右边的那个点，那么题目就是在要求我们选出的区间要满足区间[l, r]内所有颜色的max(rr[i]) <= r,并且min(ll[i]) >= l. 因为是区间相关的问题，又涉及到左右端点，因此我们考虑扫描线，那么考虑如何维护它。

　　因为每个颜色的ll[i]和rr[i]可以看做构成了一个区间，那么现在已经进入线段树的节点就分2种情况。

　　1，区间右端点超过当前右端点：

　　　　

　　我们找到离当前右端点最近的点x，使得它代表的区间和右端点关系如上图所示，那么显然这个点x以及它之前的左端点都是不能取的，又因为这个点x是离当前右端点最近的满足条件的点，所以这个点之后都不会因为这个条件而产生冲突，即在这个点后面的，在当前右端点前面的，都满足了右端点的限制。那么我们只需要再满足左端点的限制，然后查询(x, i)对答案的贡献，其中i是当前枚举的右端点。那么我们如何找这个点呢？

　　观察到一个性质，在后面出现的点的右端点>= 前面出现的点的右端点 的情况下，在后面出现的肯定会更优；因此我们只需要维护一个右端点单调递减的单调栈即可，如果有一个右端点更右出现了，那么肯定会比之前右端点比它小（相等）的点更优，但是不能弹掉右端点比它大的，因为随着右端点的增大，可能这个点就失效了，但之前右端点比它大的点还是有效的。　　　　

　　2，区间右端点不超过当前右端点。

　　　　

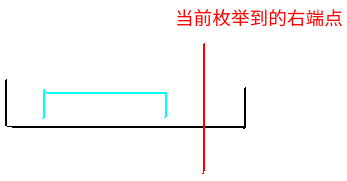
　　对于这种情况而言，显然我们要么把这个区间全部取了，要么一点都不取。因此不合法的左端点就是(ll, rr],把这段赋0即可。观察到因为我们是赋0，不是-1，所以无法撤销，但是这是没有关系的，因此如果在当前右端点下，这个区间已经不超过它了，那么以后随着右端点的增大，就更不可能超过了，因此不需要撤回。同时也正是因为无法撤回，所以上面那种情况需要单调栈而不是直接修改，因为上面那种情况，随着右端点的增大，是会变成第二种情况的。

 #include<bits/stdc++.h>
 using namespace std;
 #define R register int
 #define AC 301000
 #define ac 1200100
 #define LL long long

 /*用栈来维护查询的区间（因为每次的区间不同，而且都只要修改前缀，所以完全不用每次修改
 （修改了就无法转移到下一个右端点了，因为不满足区间减法，无法撤销），
 只需要查询指定区间内的就可以了*/

 int n, tot, T;
 LL ans;
 int ll[AC], rr[AC], color[AC];
 int s[AC], top;//栈
 int tree[ac], lazy[ac], l[ac], r[ac];//线段树
 struct co{
     int color, id;
 }p[AC];

 struct seg{
     int l, r;
 }line[AC];

 bool z[AC];

 inline int read()
 {
     int x = ;char c = getchar();
     while(c > '' || c < '') c = getchar();
     while(c >= '' && c <= '') x = x *  + c - '', c = getchar();
     return x;
 }

 inline bool cmp1(seg a, seg b)
 {
     return a.r < b.r;
 }

 inline bool cmp(co a, co b)
 {
     if(a.color != b.color) return a.color < b.color;
     else return a.id < b.id;
 }

 inline void pushdown(int x)
 {
     if(l[x] != r[x] && lazy[x])
     {
         int ll = x * , rr = ll + ;
         tree[ll] = tree[rr] = lazy[x] = ;
         lazy[ll] = lazy[rr] = ;
     }
 }

 inline void update(int x)
 {
     tree[x] = tree[x * ] + tree[x *  + ];
 }

 void build(int x, int ll, int rr)
 {
     l[x] = ll, r[x] = rr, lazy[x] = ;
     if(ll == rr) {tree[x] = ; return ;}
     int mid = (ll + rr) >> ;
     build(x * , ll, mid), build(x *  + , mid + , rr);
     update(x);
 }

 void change(int x, int ll, int rr)
 {
     pushdown(x);
     if(l[x] == ll && r[x] == rr) {tree[x] = , lazy[x] = ; return ;}
     int mid = (l[x] + r[x]) >> ;
     if(rr <= mid) change(x * , ll, rr);
     else if(ll > mid) change(x *  + , ll, rr);
     else change(x * , ll, mid), change(x *  + , mid + , rr);
     update(x);
 }

 void find(int x, int ll, int rr)
 {
     pushdown(x);
     if(l[x] == ll && r[x] == rr){ans += tree[x]; return ;}
     int mid = (l[x] + r[x]) >> ;
     if(rr <= mid) find(x * , ll, rr);
     else if(ll > mid) find(x *  + , ll, rr);
     else find(x * , ll, mid), find(x *  + , mid + , rr);
     update(x);
 }

 void pre()
 {
     n = read();
     for(R i = ; i <= n; i ++) color[i] = p[i].color = read(), p[i].id = i;
     sort(p + , p + n + , cmp);
     for(R i = ; i <= n; i ++)
         if(p[i].color != p[i - ].color)
             rr[p[i - ].color] = p[i - ].id, ll[p[i].color] = p[i].id;
     rr[p[n].color] = p[n].id;
     for(R i = ; i <= n; i ++)
         if(ll[i]) line[++tot] = (seg){ll[i], rr[i]};
     sort(line + , line + tot + , cmp1);
 }

 void init()
 {
     memset(ll, , sizeof(ll)), memset(rr, , sizeof(rr));
     tot = ans = top = ;
 }

 void get()
 {
     int l = ;
     for(R i = ; i <= n; i ++)//不断扩大右端点
     {
         //printf("!!!%d\n", i);
         while(top && rr[color[i]] >= rr[color[s[top]]]) -- top;//如果一个点在栈顶右侧，且右端点大于等于栈顶，那么它肯定更优。
         s[++top] = i;//栈里面存颜色就够了, ，，，不，，，还是需要存下标
         while(top && rr[color[s[top]]] <= i) -- top;//去掉不合法的情况
         for(; line[l].r <= i && l <= tot; ++ l)//error!!!这里要用tot，不然的话用n可能会用到一些未被覆盖的，来自前面的数据的区间
             if(line[l].l < line[l].r) change(, line[l].l + , line[l].r);
         if(s[top] +  <= i) find(, s[top] + , i); //要有合法的情况才查询，否则没有必要查询
     }
     printf("%lld\n", ans);
 }

 void work()
 {
     T = read();
     while(T --) init(), pre(), build(, , n), get();
 }

 int main()
 {
 //    freopen("color7.in", "r", stdin);
     work();
 //    fclose(stdin);
     return ;
 }