计算机码

计算机在实际存储数据的时候，是采用编码规则的（二进制编码）

计算机码存储的过程： 原码、反码和补码，数值最左边一位用来充当符号位：符号为正数为0，负数为1

原码：数据本身从十进制转换为二进制的值

----正数：左边符号位为0

----负数：左边符号位为1

反码：针对负数，符号位不变，其他位取反

补码：针对负数，反码 + 1

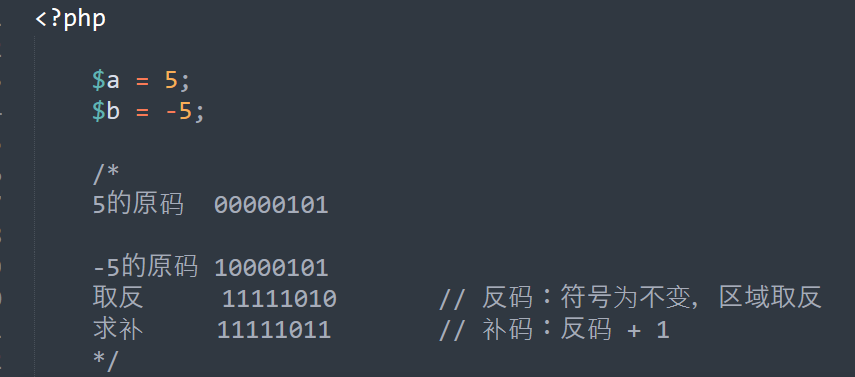
示例：

位运算

位运算符

运算符
& 按位于 两个为都为1，则返回1，否者都是0
| 按位或 两个有一个为1，返回1，
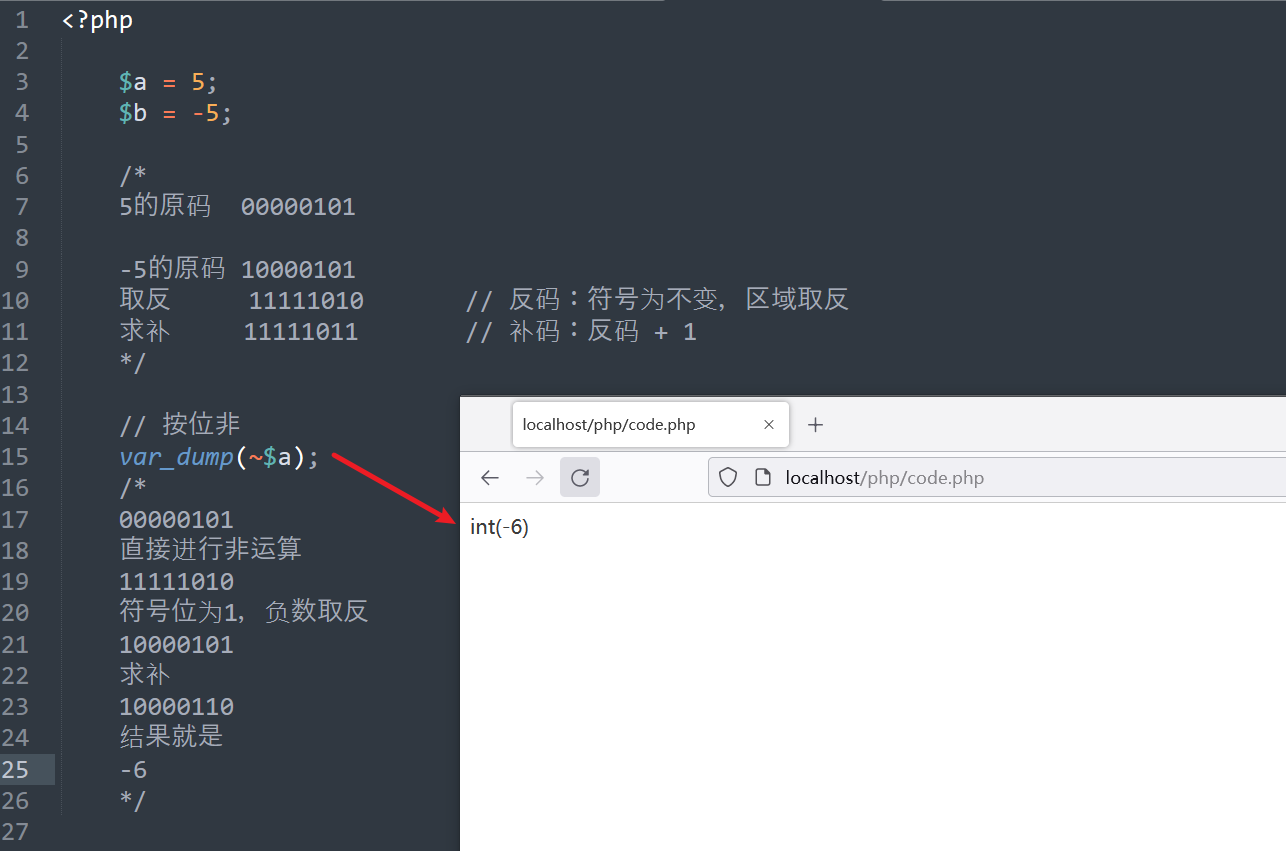
~ 按位取反 0转换为1,1转换为0
^ 按位异或 两个相同则为0，不同为1
<<< 按位左移 整个位(32)位，向左移动一位，右边补0
>>> 按位右移 整个位，向右移动一位，左边补符号位（正数补0,负数补1）

具体看示例：

按位与

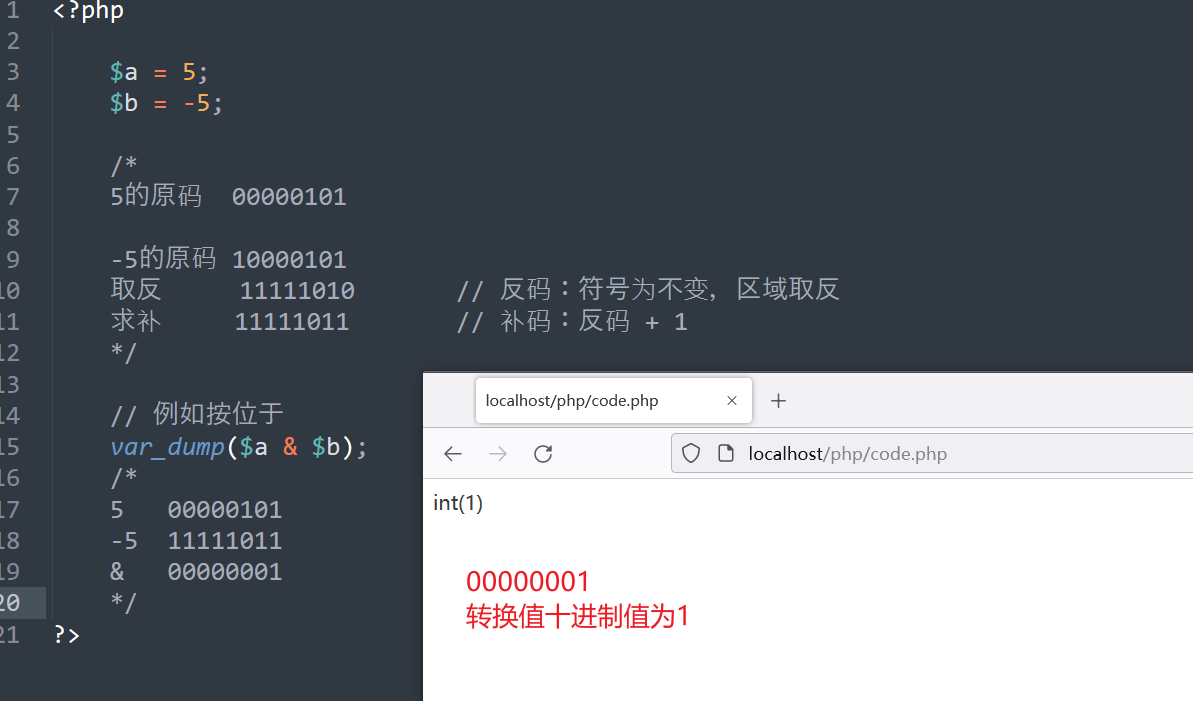
按位或

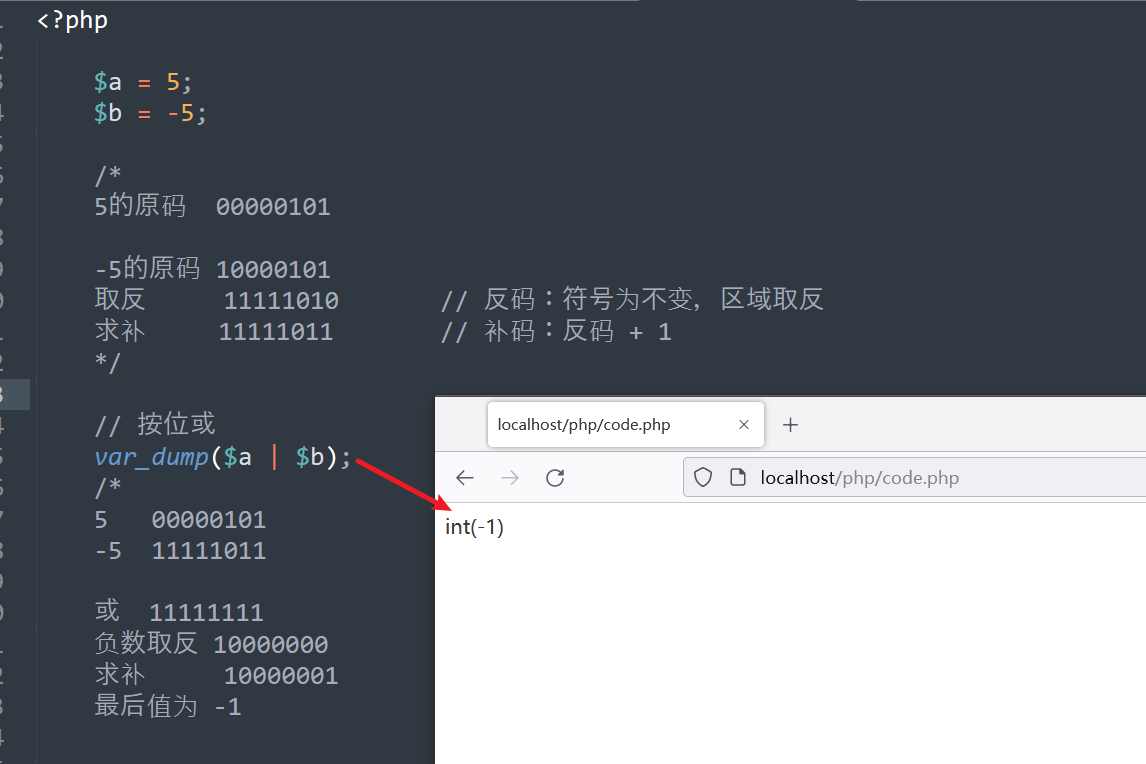
按位非

按位异或

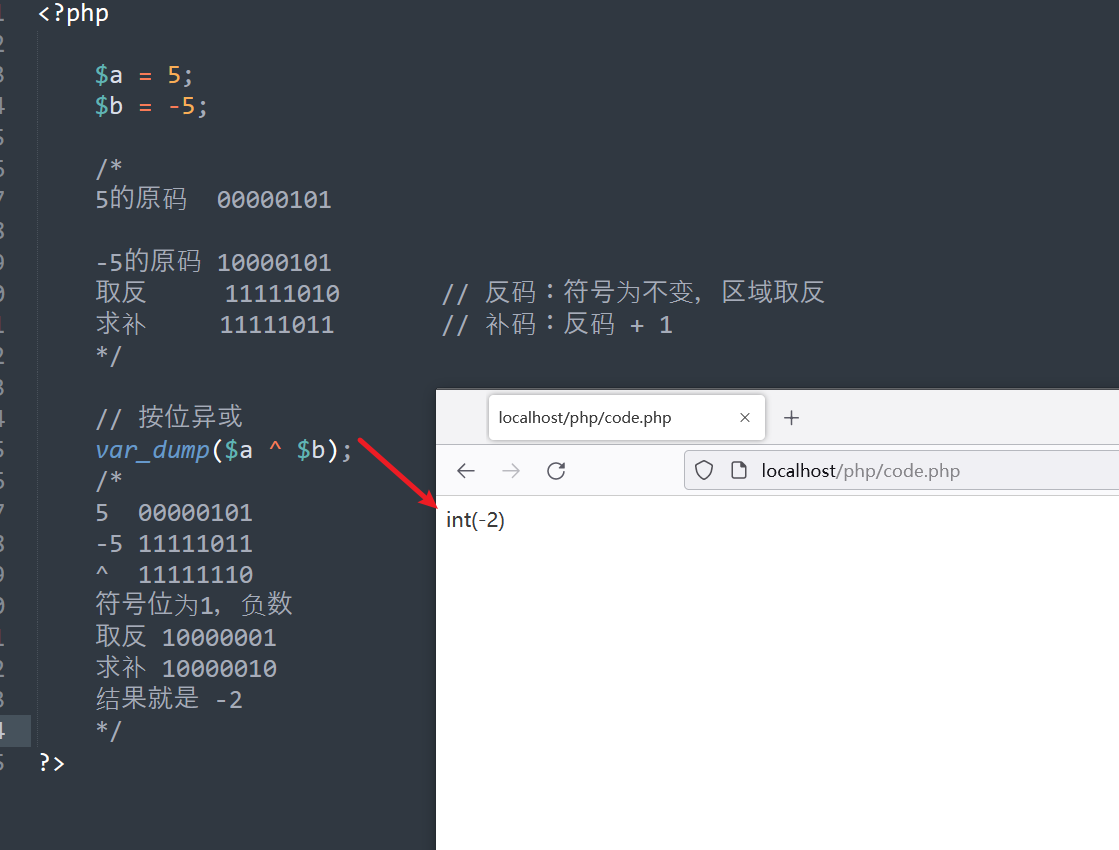
按位右移

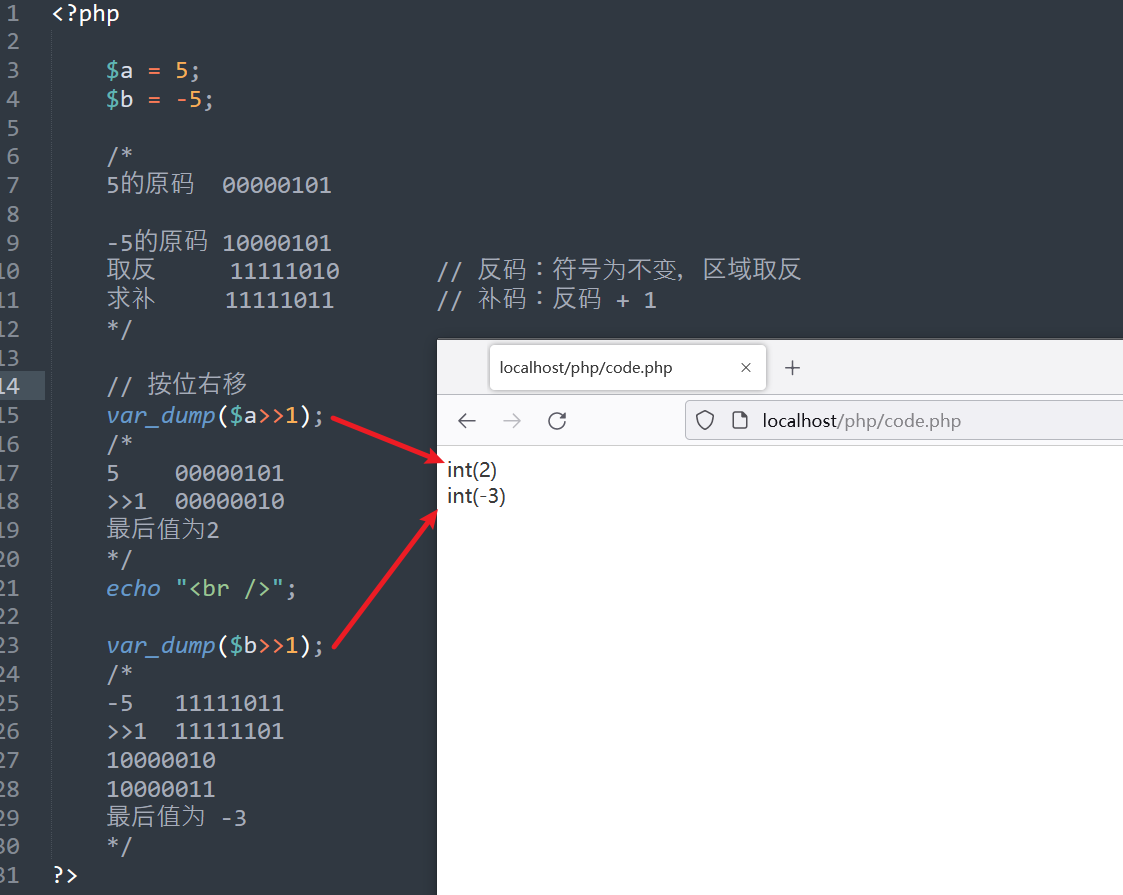
按位左移

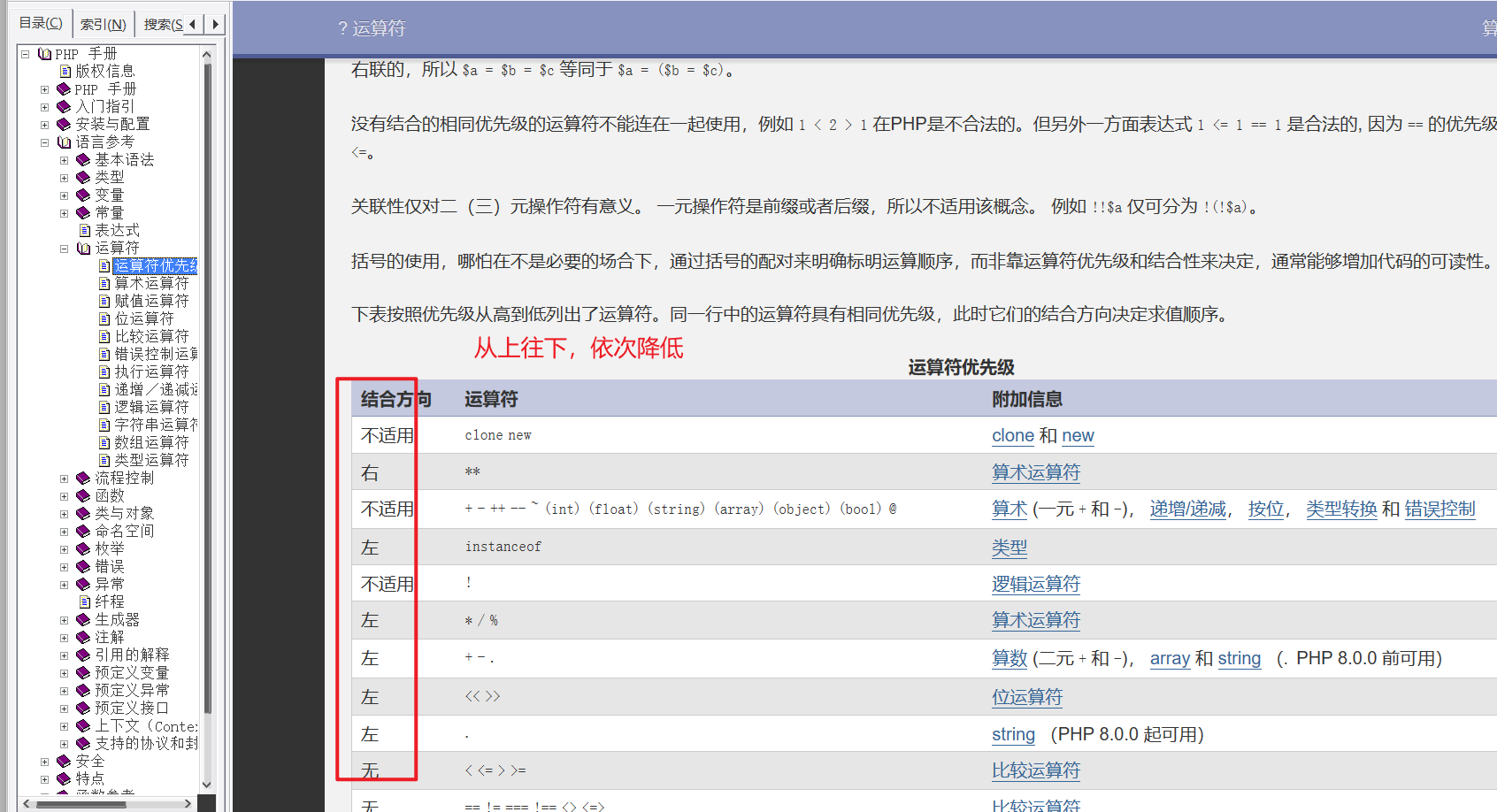
运算符优先级

同时进行多个运算符，如何运算

PHP 计算机码、位运算、运算符优先级的更多相关文章

  1. 数据运算+-*/,比较运算符==!=,赋值运算,逻辑运算and,or,not,成员运算in,not in,身份运算is is not,位运算&|,运算符的优先级

    取模就是返回余数. 取模的作用主要是来取奇偶数来用的,奇数干嘛,偶数干嘛. 比较运算符: 赋值运算: 逻辑运算: 赋值的时候可以多个变量同时赋值 成员运算: in就是在不在的意思. 身份运算: 位运算 ...

  2. POJ 1753 位运算+枚举

    题意: 给出4*4的棋盘,只有黑棋和白棋,问你最少几步可以使棋子的颜色一样. 游戏规则是:如果翻动一个棋子,则该棋子上下左右的棋子也会翻一面,棋子正反面颜色相反. 思路: 都是暴搜枚举. 第一种方法: ...

  3. STL+位运算的文件

    1.queue 队列 queue的头文件是<queue>. 定义queue对象的示例代码如: queue<int>q;  队列内存放的是int类型的数 queue<dou ...

  4. leetcode 231 Power of Two（位运算）

    Given an integer, write a function to determine if it is a power of two. 题解:一次一次除2来做的话,效率低.所以使用位运算的方 ...

  5. 为什么Java的hash表的长度一直是2的指数次幂？为什么这个(hash&(h-1)=hash%h)位运算公式等价于取余运算？

    1.什么是hash表? 答:简单回答散列表,在hash结构散列(分散)存放的一种数据集结构. 2.如何散列排布,如何均匀排布? 答:取余运算 3.Java中如何实现? 答:hash&(h-1) ...

  6. N皇后-位运算优化

    N皇后问题 时间限制: 5 Sec  内存限制: 128 MB 题目描述 魔法世界历史上曾经出现过一个伟大的罗马共和时期,出于权力平衡的目的,当时的政治理论家波利比奥斯指出:“事涉每个人的权利,绝不应 ...

  7. 为什么位运算可以实现加法（1、 不考虑进位的情况下位运算符中的异或^可以表示+号）（2、 位运算符中的与运算符&和左移运算符<<可以模拟加法中的进位）（3、位运算不仅可以做加法，还可以做其它的乘法减法等：计算机本质是二进制运算）

    为什么位运算可以实现加法(1. 不考虑进位的情况下位运算符中的异或^可以表示+号)(2. 位运算符中的与运算符&和左移运算符<<可以模拟加法中的进位)(3.位运算不仅可以做加法,还 ...

  8. JAVA:二进制(原码 反码 补码)，位运算，移位运算，约瑟夫问题（5）

    一.二进制,位运算,移位运算 1.二进制 对于原码, 反码, 补码而言, 需要注意以下几点: (1).Java中没有无符号数, 换言之, Java中的数都是有符号的; (2).二进制的最高位是符号位, ...

  9. Java学习第五篇:二进制(原码 反码 补码)，位运算，移位运算，约瑟夫问题

    一.二进制,位运算,移位运算 1.二进制 对于原码, 反码, 补码而言, 需要注意以下几点: (1).Java中没有无符号数, 换言之, Java中的数都是有符号的; (2).二进制的最高位是符号位, ...

  10. 全国计算机等级考试二级教程-C语言程序设计_第15章_位运算

    位运算,不适用于实数,仅仅适用于整数.字符. C语言的位运算只能操作整数.字符,实数是指数方式表示的,不适用于位运算. #define _CRT_SECURE_NO_WARNINGS #include ...

随机推荐

  1. 杭电oj 求数列的和

    Problem Description 数列的定义如下:数列的第一项为n,以后各项为前一项的平方根,求数列的前m项的和.   Input 输入数据有多组,每组占一行,由两个整数n(n<10000 ...

  2. 删除没有刀路的刀具.txt

      1 UF_initialize(); 2 std::vector<tag_t>tool_tag; 3 std::vector<tag_t>del_tag; 4 tag_t ...

  3. Mysql学习：1、mysql安装及配置及连接Navicat

    1.下载地址: https://dev.mysql.com/downloads/windows/installer/8.0.html 2.安装流程: a.选自定义安装:custom. b. 在下一步的 ...

  4. Linux 使用Samba或NFS实现文件共享

    SAMBA文件共享服务 Samba是一款开源的文件共享软件,经过简单配置就能够实现Linux系统与Windows系统之间的文件共享工作. 例1:配置Samba服务前,先删掉Samba服务主配置文件中的 ...

  5. 25 bootstrap--v3--datetimepicker时间选择器--应用

    在模板中引用响应的文件 比如: layout.html <link rel="stylesheet" href="{% static 'stark/plugins/ ...

  6. vantUI <van-uploader> 上传图片，如何获取图片的尺寸

    html代码 <van-uploader preview-size="300px" style="width:300px;display:block;margin: ...

  7. JavaScript 取消事件的默认动作

    preventDefault() 方法 Event 对象 定义和用法 取消事件的默认动作. 语法 event.preventDefault() 说明 该方法将通知 Web 浏览器不要执行与事件关联的默 ...

  8. docker build提示 error checking context：can't stat xxx

    这个提示基本是权限不够外加目录结构不对,保险的做法直接删除 Dockerfile. 正确做法:(可能还有其他的解决方案吧,这个可以生效) 重新建个目录,给目录授权,然后再dockerfile文件夹中建 ...

  9. 如何卸载powermill？怎么把powermill彻底卸载删除干净重新安装的方法【转载】

    如何卸载powermill?怎么把powermill彻底卸载删除干净重新安装的方法.powermill显示已安装或者报错出现提示安装未完成某些产品无法安装的问题,怎么完全彻底删除清理干净powermi ...

  10. Shell写脚本关于ssh执行jar包，需要刷新JDK路径的问题

    比如脚本中下面这一段 ssh $i "java -jar /applog/$PROJECT/$APPNAME --server.port=$SERVER_PORT >/dev/null ...