网络流—最大流（Edmond-Karp算法）

一、含义

　　从源点到经过的所有路径的最终到达汇点的所有流量和

　　例如：

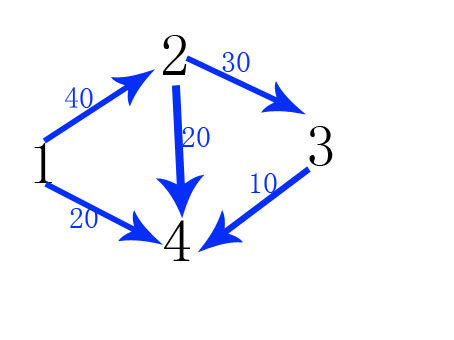
　　在这个图中求源点1，到汇点4的最大流。答案为50，其中1->2->4为20 ；1->4为20 ；1->2->3->4为10；总和为20+20+10=50。

二、EK算法的核心

　　反复寻找源点s到汇点t之间的增广路径，若有，找出增广路径上每一段[容量-流量]的最小值delta，若无，则结束。
　　在寻找增广路径时，可以用BFS来找，并且更新残留网络的值(涉及到反向边)。
　　而找到delta后，则使最大流值加上delta，更新为当前的最大流值。

对于BFS找增广路：

1.     flow[1]=INF，pre[1]=0;

源点1进队列，开始找增广路，

　　capacity[1][2]=40>0，则flow[2]=min(flow[1],40)=40;

capacity[1][4]=20>0,则flow[4]=min(flow[1],20)=20;

capacity[2][3]=30>0,则flow[3]=min(folw[2]=40，30)=30；

capacity[2][4]=30,但是pre[4]=1(已经在capacity[1][4]这遍历过4号点了)

capacity[3][4].....

当index=4（汇点），结束增广路的寻找

传递回increasement（该路径的流），利用前驱pre寻找路径

　　 路径也自然变成了这样：

2.flow[1]=INF，pre[1]=0;

源点1进队列，开始找增广路，

　　capacity[1][2]=40>0，则flow[2]=min(flow[1],40)=40;

capacity[1][4]=0!>0,跳过

capacity[2][3]=30>0,则flow[3]=min(folw[2]=40，30)=30；

capacity[2][4]=30,pre[4]=2，则flow[2][4]=min(flow[2]=40,20)=20;

capacity[3][4].....

当index=4（汇点），结束增广路的寻找

传递回increasement（该路径的流），利用前驱pre寻找路径

图也被改成

接下来同理

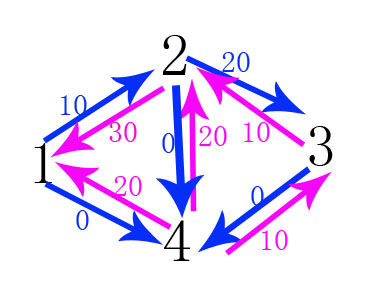
这就是最终完成的图，最终sumflow=20+20+10=50（这个就是最大流的值）

PS，为什么要有反向边呢？

我们第一次找到了1-2-3-4这条增广路，这条路上的delta值显然是1。于是我们修改后得到了下面这个流。（图中的数字是容量）

这时候(1,2)和(3,4)边上的流量都等于容量了，我们再也找不到其他的增广路了，当前的流量是1。

但这个答案明显不是最大流，因为我们可以同时走1-2-4和1-3-4，这样可以得到流量为2的流。

那么我们刚刚的算法问题在哪里呢？问题就在于我们没有给程序一个”后悔”的机会，应该有一个不走(2-3-4)而改走(2-4)的机制。那么如何解决这个问题呢？回溯搜索吗？那么我们的效率就上升到指数级了。

而这个算法神奇的利用了一个叫做反向边的概念来解决这个问题。即每条边(I,j)都有一条反向边(j,i)，反向边也同样有它的容量。

我们直接来看它是如何解决的：

在第一次找到增广路之后，在把路上每一段的容量减少delta的同时，也把每一段上的反方向的容量增加delta。即在Dec(c[x,y],delta)的同时，inc(c[y,x],delta)

我们来看刚才的例子，在找到1-2-3-4这条增广路之后，把容量修改成如下

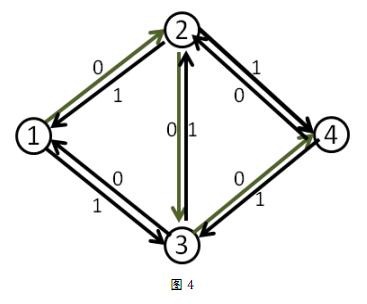
这时再找增广路的时候，就会找到1-3-2-4这条可增广量，即delta值为1的可增广路。将这条路增广之后，得到了最大流2。

那么，这么做为什么会是对的呢？我来通俗的解释一下吧。

事实上，当我们第二次的增广路走3-2这条反向边的时候，就相当于把2-3这条正向边已经是用了的流量给”退”了回去，不走2-3这条路，而改走从2点出发的其他的路也就是2-4。（有人问如果这里没有2-4怎么办，这时假如没有2-4这条路的话，最终这条增广路也不会存在，因为他根本不能走到汇点）同时本来在3-4上的流量由1-3-4这条路来”接管”。而最终2-3这条路正向流量1，反向流量1，等于没有流量。

这就是这个算法的精华部分，利用反向边，使程序有了一个后悔和改正的机会。而这个算法和我刚才给出的代码相比只多了一句话而已。

至此，最大流Edmond-Karp算法介绍完毕。

三、代码：

/*poj1273*/
#include <iostream>
#include <cstdlib>
#include <algorithm>
#include <string>
#include <cstring>
#include <stdio.h>
#include <queue>
#define IO ios::sync_with_stdio(false);\
    cin.tie();\
    cout.tie();
using namespace std;
const int MAX=;
int map[][],flow[],pre[],n,m;
bool vis[];
int BFS()
{
    int up;
    queue<int> q;
    vis[]=;
    memset(pre,-,sizeof(pre));
    memset(vis,,sizeof(vis));
    for(int i=; i<=n; i++)
        flow[i]=MAX;
    q.push();
    while(!q.empty())
    {
        up=q.front();
        q.pop();
        if(up==n)
            break;
        for(int i=; i<=n; i++)
        {
            if(!vis[i]&&map[up][i]>)
            {
                vis[i]=;
                flow[i]=min(flow[up],map[up][i]);
                pre[i]=up;
                q.push(i);
            }
        }
    }
    if(!vis[n]||n==)
        return -;
    return flow[n];
}
int EK()
{
    int d,maxflow=,up,down;
    maxflow=;
    while((d=BFS())!=-)
    {
        maxflow+=d;
        down=n;
        while(down!=)
        {
            up=pre[down];
            map[up][down]-=d;
            map[down][up]+=d;
            down=up;
        }
    }
    return maxflow;
}
int main()
{
    while(~scanf("%d%d",&m,&n))
    {
        memset(map,,sizeof(map));
        int a,b,c;
        for(int i=; i<=m; i++)
        {
            scanf("%d%d%d",&a,&b,&c);
            map[a][b]+=c;
        }
        printf("%d\n",EK());//输出从1到n号点的最大流
    }
    return ;
}