【9.15校内测试】【寻找扩展可行域+特判】【Trie树 异或最小生成树】【模拟:)】

之前都没做出来的同名题简直留下心理阴影啊...其实这道题还是挺好想的QAQ

可以发现，鸟可以走到的点是如下图这样扩展的：

由$(0,0)$向两边扩展，黑色是可以扩展到的点，红色是不能扩展的点，可以推出，在扩展的区间内，横纵坐标奇偶性相同的点就可以被扩展到，反之则一定不可以。

接下来看有柱子的情况：

可以发现，遇到柱子时，可行的区域就变成了与柱子的区域取交集，然后接着向后扩展，直到遇到下一个柱子。

我们最后要找的实际上就是横坐标为$m$时可行区域的下界，可以证明到下界按的次数一定是最少的。而求到一个点需要按的次数就直接用$(x+y)/2$就可以叻。

【注意】当当前范围左右端点不可行时要缩小范围。

#include<iostream>
#include<cstdio>
using namespace std;

long long read ( long long & x ) {
    x = ; char ch = getchar ( ); int t = ;
    while ( ch > '' || ch < '' ) { if ( ch == '-' ) t = -; ch = getchar ( ); }
    while ( ch >= '' && ch <= '' ) { x = x *  + ch - ''; ch = getchar ( ); }
    x = x * t;
}

long long p, q, m, n;
long long pos[], b[], c[], L[], R[];
int main ( ) {
    freopen ( "bird.in", "r", stdin );
    freopen ( "bird.out", "w", stdout );
    scanf ( "%lld%lld%lld%lld", &p, &q, &m, &n );
    for ( int i = ; i <= n; i ++ )
        read ( pos[i] ), read ( b[i] ), read ( c[i] );
    if ( q - p ==  ) {
        printf ( "-1" ); return ;
    }
    int i;
    long long l, r;
    for ( i = ; i <= n && pos[i] <= m; i ++ ) {
        L[i] = L[i-] - ( pos[i] - pos[i-] );
        R[i] = R[i-] + ( pos[i] - pos[i-] );
        L[i] = max ( b[i] + , L[i] );
        R[i] = min ( c[i] - , R[i] );
        if ( pos[i] %  ) {
            if ( L[i] %  ==  ) L[i] += ;
            if ( R[i] %  ==  ) R[i] -= ;
        } else {
            if ( L[i] %  ) L[i] += ;
            if ( R[i] %  ) R[i] -= ;
        }
        if ( L[i] > R[i] ) { printf ( "-1" ); return ; }
    }
    i --;
    l = L[i] - ( m - pos[i] );
    r = R[i] + ( m - pos[i] );
    l = max ( p + , l );
    r = min ( q - , r );
    if ( m %  ) {
        if ( l %  ==  ) l += ;
        if ( r %  ==  ) r -= ;
    } else {
        if ( l %  ) l += ;
        if ( r %  ) r -= ;
    }
    if ( l > r ) { printf ( "-1" ); return ; }
    else printf ( "%lld", ( l + m ) >>  );
    return ;
}

关于按位运算的总是和$Trie$树有关啊...

可是考场上怎么也想不到怎么利用$Trie$树处理最小生成树。

最后发现原理其实还是挺简单的，就是代码实现...（最后用自己的写法$A$掉叻简直无敌激动啊！！

首先把所有数建成一棵$Trie$树，如下：

上图表示了1到7的所有数（统一位数后），可以发现，在叶子节点位置的相邻两个相连一定是当前最优的连法，因为这样连的代价一定是1：

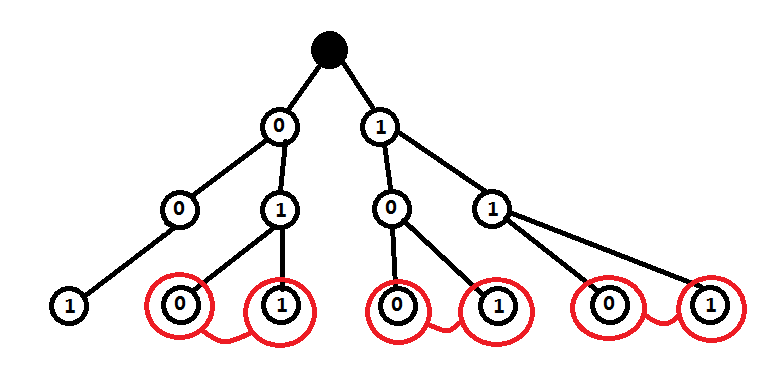
于是现在要向上走合并两个子树：

比如合并如上子树时，实际上是要在两个子树中各找一个数，使这两个树的异或值是当前最小的。而且合并相邻两个子树一定比跳子树合并要优，相当于保证了前面位数一样，只看后面不一样的部分，相邻的子树前面一样的部分一定是最优的。

于是问题转换为如何快速在两个子树中找到异或值最小的两个数。暴力就是$n^2$复杂度。

然后我们想到如果是给定一个值，要在一个$Trie$树上找到与之异或起来最小的树，就是沿着$Trie$树，按位往最优的走就可以了，复杂度是$log_{位数}$。

所以回到题上，我们可以遍历一个子树的所有数，在另外一个子树上$log$查找最优解，成功将复杂度简化为$nlog_n$。

在此我采用$dfs$遍历子树（选择遍历的子树是$size$小的那一个），根据深度来判断是否到底和在路上计算异或。

（自己写出来还是挺感动的55555

（尝试了一下新的代码风格

#include<bits/stdc++.h>
using namespace std;

int n, a[];

int son[][], tail;
long long ans, vmin;
int siz[], dep[];
void build(int x, int id) {
    int u = ;
    int t = ;
    while(t >= ) {
        int now = ( x >> t ) & ;
        if(!son[u][now]) {
            son[u][now] = ++tail;
            siz[u] ++;
            dep[tail] = t;
        }
        u = son[u][now];
        t --;
    }
    return;
}

long long query(long long val, int nd, long long now) {
    if(!dep[nd])    return now;
    int t = (val >> (dep[nd] - )) & ;
    if(son[nd][t])    return query(val, son[nd][t], now << );
    else    return query(val, son[nd][t^], now <<  | );
}

void Find(int nd, long long val, int rs) {
    if(!dep[nd]) { vmin = min(vmin, query(val, rs, )); return; }
    if(son[nd][])    Find(son[nd][], val << , rs);
    if(son[nd][])    Find(son[nd][], val <<  | , rs);
}

void Dfs ( int u ) {
    int ls = son[u][], rs = son[u][];
    if(ls)    Dfs(ls);
    if(rs)    Dfs(rs);
    if(!ls || !rs)    return;
    if(siz[ls] > siz[rs])    swap(ls, rs);
    vmin = 0x3f3f3f3f;
    Find(ls, ls == son[u][], rs);
    ans += vmin;
} 

int main ( ) {
    freopen("road.in", "r", stdin);
    freopen("road.out", "w", stdout);
    scanf("%d", &n);
    for ( int i = ; i <= n; i ++ ) {
        scanf("%d", &a[i]);
        build(a[i], i);
    }
    Dfs();
    printf("%lld", ans);
    return ;
}

这是我在考试中见过最长的题干了...

（所以当然不会改的，以下是$std$133行代码%%%

（真的是不能接受这种抽象的码风！！

#define FIO "code"
#include <cstdio>
#include <cctype>
#define L_MAX 112640
#define O_MAX 55
#define N_MAX 56
#define C_MAX 127
inline bool is_name(int c)
{
    return isalnum(c) || c == '_' || c == '$';
}
char a[L_MAX + ],
    * i = a, * j = i, * k = a, * l = k; // [i, j): last word; [k, l): current word
const char * op[O_MAX] = {
    "((", "))", "[[", "[<:", "]]", "]:>", "{{", "{<%", "}}", "}%>",
    "##", "#%:", "..", "!!", "~~", ",,", ";;",
    "++", "=+=", "+++", "--", "=-=", "---", "**", "=*=",
    "&&", "=&=", "&&&", "||", "=|=", "|||", "^^", "=^=",
    "<<", "=<=", "<<<", "=<<=", ">>", "=>=", ">>>", "=>>=",
    "==", "===", "=!=", "??", "::", ":::",
    "''", "\"\"", "//", "=/=", "c//", "C/*", "%%", "=%=",
};
int n = , trie[N_MAX + ][C_MAX], type[N_MAX + ],
    r, // is forced to break line?
    s, t; // type of [i, j), [k, l); [0] => empty, [1] => name, [c] => type
inline void insert(int t, const char * s)
{
    static int u;
    for (u = ; *s; u = trie[u][int(*s++)])
        if (!trie[u][int(*s)]) trie[u][int(*s)] = ++n;
    type[u] = t;
}
inline bool check()
{
    return s == ' ' || (s ==  && t == ) || (s == '/' && (*k == '/' || *k == '*')) || (s == ':' && *k == ':') || (s == '+' && *k == '+') || (s == '-' && *k == '-') || (s == '<' && *k == '<') || (s == '>' && *k == '>') || (s == '&' && *k == '&') || (s == '<' && *k == ':') || (s == '%' && *k == ':') || (s ==  && t == '"' && j != k && ((j - i ==  && (*i == 'u' || *i == 'U' || *i == 'L')) || (j - i ==  && *i == 'u' && *(i + ) == '')));
}
inline void output(int c = )
{
    if (c) putchar(c);
    i = k, j = l, s = t;
    while (k < l) putchar(*k++);
}
inline char seek(char * l)
{
    while (*l == '\\' && !*(l + )) gets(l);
    return *l;
}
inline void seek_char(char *& l)
{
    for (seek(l); *l != '\''; seek(++l))
        if (*l == '\\') seek(++l);
    ++l;
}
inline void seek_str(char *& l)
{
    for (seek(l); *l != '"'; seek(++l))
        if (*l == '\\') seek(++l);
    ++l;
}
inline void seek_comment_line(char *& l)
{
    for (seek(l); *l; seek(++l));
}
inline void seek_comment_block(char *& l)
{
    do
    {
        ++l;
        while (!seek(l))
            *l++ = '\n', gets(l);
        seek(l);
    }
    while (*l != '/' || *(l - ) != '*');
    ++l;
}
inline int seek_word(char *& k, char *& l)
{
    static int t, u;
    do
    {
        k = l;
        while (isspace(seek(k)))
            ++k;
        if (!*(l = k))
            t = ;
        else if (is_name(*l)) // names | numbers
            for (t = , ++l; is_name(seek(l)); ++l);
        else
        {
            for (u = ; seek(l) && trie[u][int(*l)]; u = trie[u][int(*l++)]);
            t = type[u];
            switch (t)
            {
            case '\'': seek_char(l); break;
            case '"':  seek_str(l); break;
            case 'c':  seek_comment_line(l); break;
            case 'C':  seek_comment_block(l); break;
            }
        }
    }
    while (t == 'c' || t == 'C');
    return t;
}
int main()
{
    freopen(FIO ".in", "r", stdin);
    freopen(FIO ".out", "w", stdout);
    for (int o = ; o < O_MAX; ++o)
        insert(*op[o], op[o] + );
    r = '^';
    while (gets(l))
    {
        if (r == '\n') putchar('\n'), r = s = , i = j;
        t = seek_word(k, l);
        if (k == l)
            continue;
        else if (t != '#')
            output(check() ? ' ' : );
        else
        {
            output(s ==  ?  : '\n');
            r = '\n', t = seek_word(k, l), output();
            if (*i == 'd') // is #define?
            {
                t = seek_word(k, l), output(' ');
                if (seek(l) != '(') s = ' ';// is function-like macro?
            }
        }
        while ((t = seek_word(k, l)))
            output(check() ? ' ' : );
    }
    return ;
}