曼-惠特尼U检验Mann–Whitney U Test

python机器学习-乳腺癌细胞挖掘（博主亲自录制视频）

https://study.163.com/course/introduction.htm?courseId=1005269003&utm_campaign=commission&utm_source=cp-400000000398149&utm_medium=share

机器学习,统计项目联系QQ：231469242

两个配对样本，均匀分布，非正太分布

Wilcoxon signed-rank test

曼-惠特尼U检验Mann–Whitney Test

两个独立样本，均匀分布，非正太分布

两组样本量必须大于20

例子：A方案治疗和B方案治疗是否有显著差异？a=0.05

此例子简单说明计算过程，但不准确，因为样本数必须大于20

参照使用Z分数表

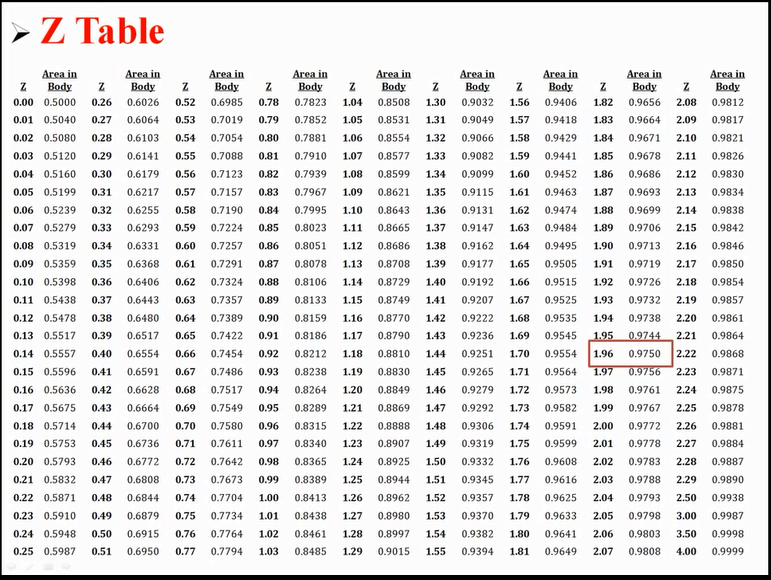
如果Z分数小于-1.96或大于1.96，拒绝原假设

计算排名

一共12个数，排名从1-12，第一12，第十二36，第四名和第五名都是19

第四名和第五名都平均为4.5

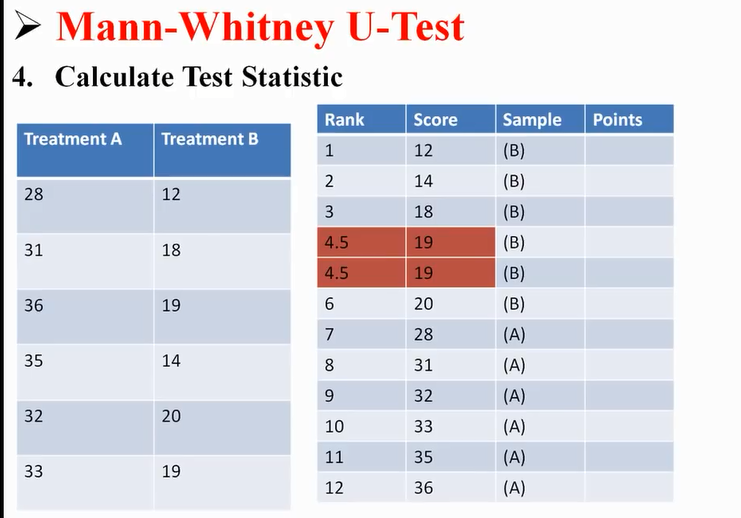
计算每个score的points

B样本的12，小于A的一个样本得1分，都小于A的样本，A的样本是6，所以得6*1=6分

A样本的28，小于B的一个样本得1分，都大于A的样本，A的样本是6，所以得6*0=0分

UA，A样本的所有points相加

UB，B样本的所有Points相加

U值取UA和UB的最小值

计算Z分数，其公式如图：

nA,nB 表示两个样本量

计算的Z值=-2.88，小于-1.96，拒绝原假设

Nonparametric Comparison of Two Groups:
Mann–Whitney Test
If the measurement values from two groups are not normally distributed we have
to resort to a nonparametric test. The most common nonparametric test for the
comparison of two independent groups is the Mann–Whitney(–Wilcoxon) test.
Watch out, because this test is sometimes also referred to as Wilcoxon rank-sum
test. This is different from the Wilcoxon signed rank sum test! The test-statistic for
this test is commonly indicated with u:

u_statistic, pVal = stats.mannwhitneyu(group1, group2)

https://github.com/thomas-haslwanter/statsintro_python/tree/master/ISP/Code_Quantlets/08_Test
sMeanValues/twoGroups.

Code: “ISP_twoGroups.py”3: Comparison of two groups, paired and unpaired.

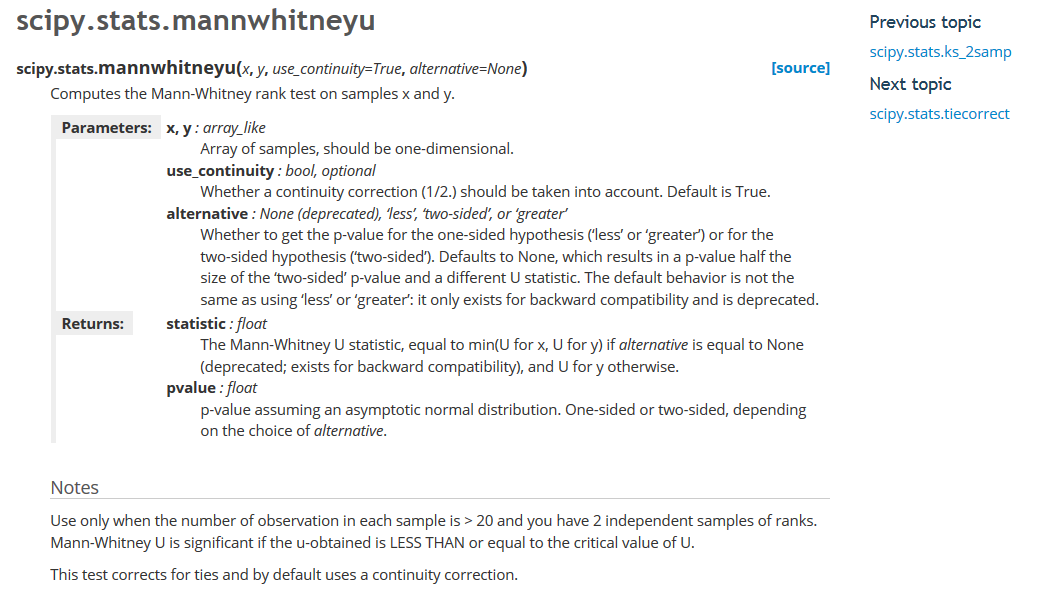
举例：

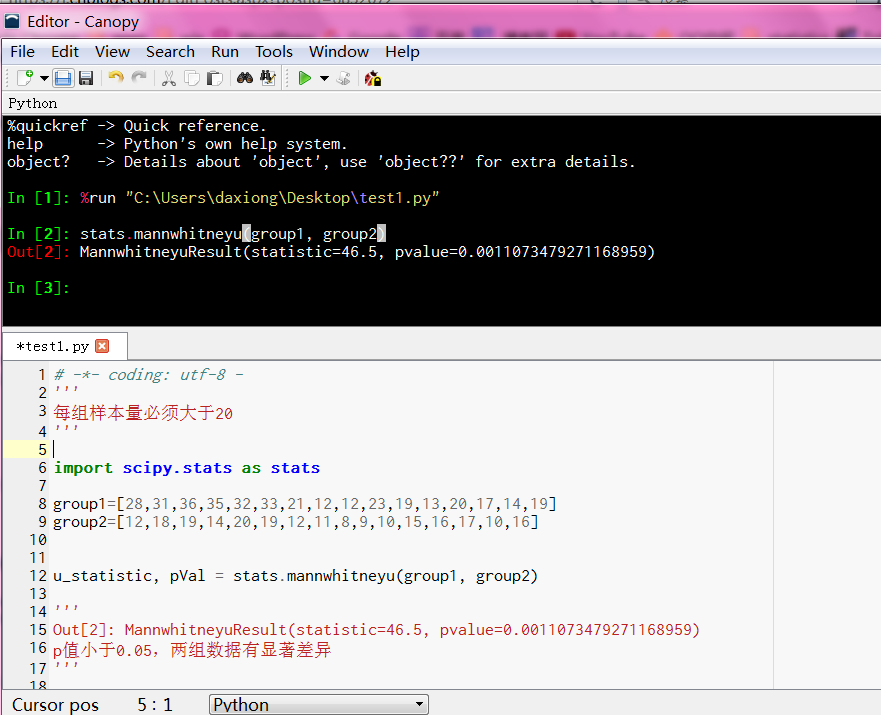
判断两组数是否有显著差异，group1=[28,31,36,35,32,33,21,12,12,23,19,13,20,17,14,19] group2=[12,18,19,14,20,19,12,11,8,9,10,15,16,17,10,16]

# -*- coding: utf-8 -
'''
每组样本量必须大于20
'''

import scipy.stats as stats

group1=[28,31,36,35,32,33,21,12,12,23,19,13,20,17,14,19]
group2=[12,18,19,14,20,19,12,11,8,9,10,15,16,17,10,16]

u_statistic, pVal = stats.mannwhitneyu(group1, group2)

'''
Out[2]: MannwhitneyuResult(statistic=46.5, pvalue=0.0011073479271168959)
p值小于0.05，两组数据有显著差异
'''
作者Toby，qq:231469242

p值小于0.05，有显著差异，拒绝原假设，两组数据有显著差异

https://study.163.com/provider/400000000398149/index.htm?share=2&shareId=400000000398149（ 欢迎关注博主主页，学习python视频资源，还有大量免费python经典文章）