【BZOJ 3561】 3561: DZY Loves Math VI （莫比乌斯，均摊log）

3561: DZY Loves Math VI

Time Limit: 10 Sec  Memory Limit: 256 MB
Submit: 205  Solved: 141

Description

给定正整数n,m。求

Input

一行两个整数n,m。

Output

一个整数，为答案模1000000007后的值。

Sample Input

5 4

Sample Output

424

HINT

数据规模：

1<=n,m<=500000，共有3组数据。

Source

By Jcvb

【分析】

　　式子已经推出来了，然而后面。。。我觉得我学了假的数论。。。

　　好吧，推式子。。

　　下面省了一些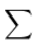

　　$$\sum_{i=1}^{n}\sum_{j=1}^{m} lcm(i,j)^{gcd(i,j)}$$

　　$$=\sum_{i=1}^{n}\sum_{j=1}^{m} {[\dfrac{i*j}{gcd(i,j)}]}^{gcd(i,j)}$$

　　$$=\sum_{d=1}^{min(n,m)}d^d \sum_{i'=1}^{n/d} \sum_{j'=1}^{m/d} (i'*j')^d [gcd(i',j')==1]$$

　　$$=\sum_{d=1}^{min(n,m)}d^d\sum_{d'=1}^{min(n,m)/d} \mu(d')\sum_{i'=1}^{\dfrac{n}{d*d'}}(i'*d')^d*\sum_{j'=1}^{\dfrac{n}{d*d'}}(j'*d')^d$$

$$如果你觉得上面难看就看下面吧$$

　　
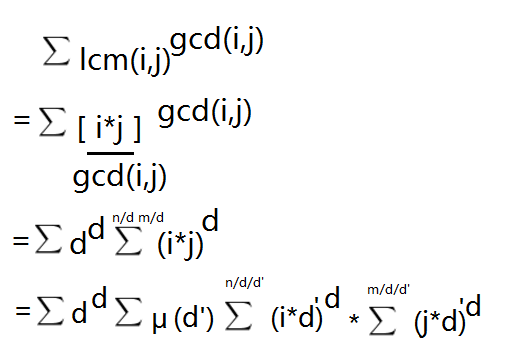
$$如果你觉得下面难看就看上面吧$$

　

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 using namespace std;
 #define Mod 1000000007
 #define Maxn 500010
 #define LL long long

 int mymin(int x,int y) {return x<y?x:y;}

 int mu[Maxn],pri[Maxn],pl;
 bool vis[Maxn];

 LL qpow(LL x,int b)
 {
     LL ans=;
     while(b)
     {
         if(b&) ans=(ans*x)%Mod;
         x=(x*x)%Mod;
         b>>=;
     }
     return ans;
 }

 void init()
 {
     pl=;
     memset(vis,,sizeof(vis));
     mu[]=;
     for(int i=;i<=Maxn-;i++)
     {
         if(!vis[i]) pri[++pl]=i,mu[i]=-;
         for(int j=;j<=pl;j++)
         {
             if(i*pri[j]>Maxn-) break;
             vis[i*pri[j]]=;
             if(i%pri[j]==) mu[i*pri[j]]=;
             else mu[i*pri[j]]=mu[i]*mu[pri[j]];
             if(i%pri[j]==) break;
         }
     }
 }

 int a[Maxn],sum[Maxn];
 void ffind(int n,int m)
 {
     int ans=;
     if(m>n) swap(m,n);
     for(int i=;i<=n;i++) a[i]=;
     for(int i=;i<=m;i++)
     {
         int x=qpow(i,i),y=;
         for(int j=;j*i<=n;j++)
         {
             a[j]=(LL)a[j]*j%Mod;
             sum[j]=(sum[j-]+a[j])%Mod;
         }
         for (int j=;j*i<=m;j++)
             y=((LL)a[j]*a[j]%Mod*sum[m/i/j]%Mod*sum[n/i/j]%Mod*mu[j]+y+Mod)%Mod;
         ans=(ans+(LL)x*y%Mod)%Mod;
     }
     printf("%d\n",ans);
 }

 int main()
 {
     int n,m;
     init();
     scanf("%d%d",&n,&m);
     ffind(n,m);
     return ;
 }

发现这个lych_cys大神的代码挺简短的，而且好像挺快的，LL都是算的时候才用。。

2017-03-23 21:56:35