C.Fountains（Playrix Codescapes Cup (Codeforces Round #413, rated, Div. 1 + Div. 2)+线段树+RMQ）

题目链接：http://codeforces.com/contest/799/problem/C

题目：

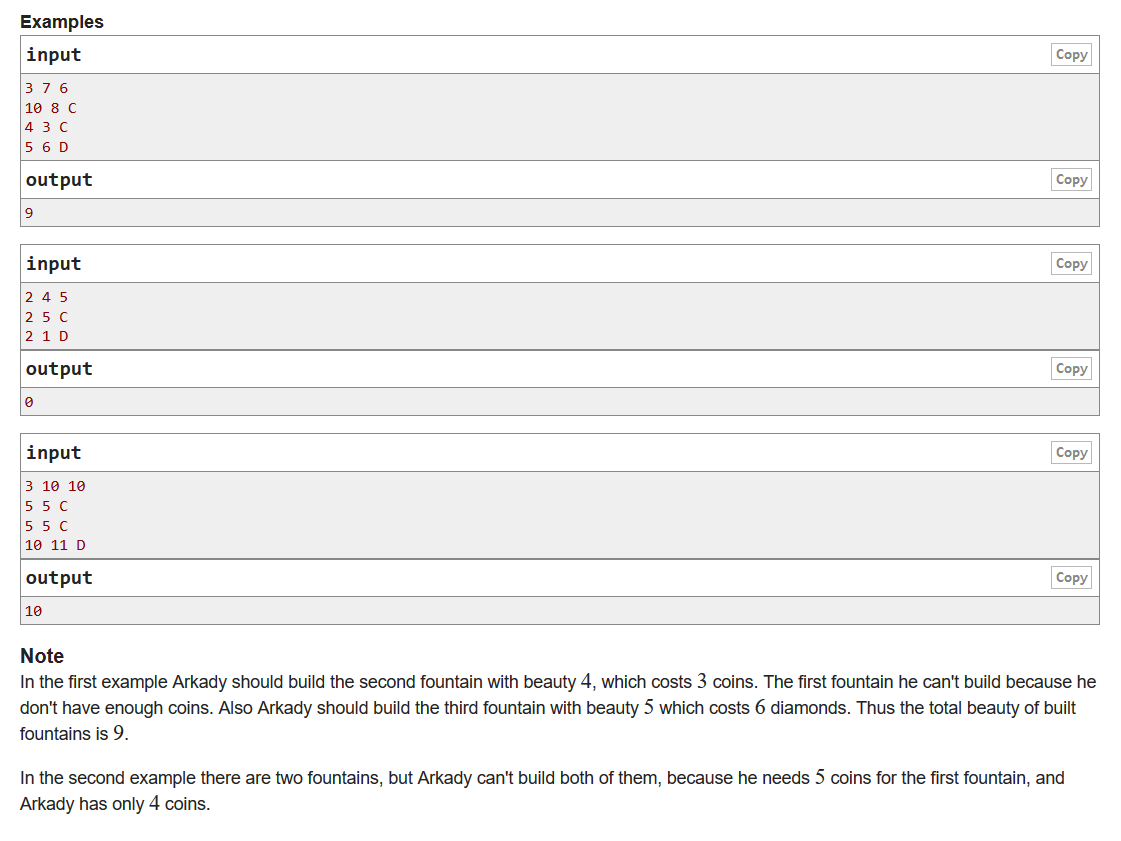
题意：

　　给你n种喷泉的价格和漂亮值，这n种喷泉题目指定用钻石或现金支付（分别用D和C表示），C和D之间不能相互转换。你现在需要修建两个喷泉，给你硬币数和现金数，问你怎样才能使修建的两个喷泉的总漂亮值最大。

思路:

　　易知，要修建的两个喷泉如果一个是用钻石支付，另一个用现金支付，那么只需找到小于给的钻石和现金的上限的漂亮值最大的两个温泉相加，此处遍历一边即可。对于这两个温泉都用同一种支付方式的情况（拿钻石支付的温泉来举例），我们可以用线段树来维护价格小于（C - 当前价格）的那些喷泉中漂亮值的最大值是多少（区间查询），当这个最大值是0时代表前面没有满足条件的喷泉，如果不是0，那么我们就看是否需要更新答案，最后我们再将当前的这个喷泉更新到线段树中（单点更新）。因为我们知道当x1+x2是最大值，那么x2+x1也一定是最大值，因此我们不排序直接这样进行查询更新是非常合理的。

代码实现如下：

 #include <set>
 #include <map>
 #include <queue>
 #include <stack>
 #include <cmath>
 #include <ctime>
 #include <bitset>
 #include <cstdio>
 #include <string>
 #include <vector>
 #include <cstdlib>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 using namespace std;

 typedef long long ll;
 typedef pair<ll, ll> pll;
 typedef pair<ll, int> pli;
 typedef pair<int, ll> pil;;
 typedef pair<int, int> pii;
 typedef unsigned long long ull;

 #define lson i<<1
 #define rson i<<1|1
 #define bug printf("*********\n");
 #define FIN freopen("D://code//in.txt", "r", stdin);
 #define debug(x) cout<<"["<<x<<"]" <<endl;
 #define IO ios::sync_with_stdio(false),cin.tie(0);

 const double eps = 1e-;
 const int mod = ;
 const int maxn = 1e5 + ;
 const double pi = acos(-);
 const int inf = 0x3f3f3f3f;
 const ll INF = 0x3f3f3f3f3f3f3f;

 int n, c, d, bea, cost, mx1, mx2, t1, t2;
 char op[];

 struct node {
     int bea, cost;
     node(int bea = , int  cost = ) : bea(bea), cost(cost) {}
 }num1[maxn], num2[maxn];

 struct tree {
     int l, r, mx;
 }segtree[maxn*];

 void push_up(int i) {
     segtree[i].mx = max(segtree[i*].mx, segtree[i*+].mx);
 }

 void build(int i, int l, int r) {
     segtree[i].l = l, segtree[i].r = r;
     if(l == r) {
         segtree[i].mx = ;
         return;
     }
     int mid = (l + r) >> ;
     build(i * , l, mid);
     build(i *  + , mid + , r);
     push_up(i);
 }

 void update(int i, int pos, int val) {
     if(segtree[i].l == pos && segtree[i].r == pos) {
         segtree[i].mx = max(segtree[i].mx, val);
         return;
     }
     int mid = (segtree[i].l + segtree[i].r) >> ;
     if(pos <= mid) update(i*, pos, val);
     else update(i*+, pos, val);
     push_up(i);
 }

 int query(int i, int l, int r) {
     if(segtree[i].l == l && segtree[i].r == r) {
         return segtree[i].mx;
     }
     int mid = (segtree[i].l + segtree[i].r) >> ;
     if(r <= mid) return query(i*, l, r);
     else if(l > mid) return query(i*+, l, r);
     else return max(query(i*, l, mid), query(i*+, mid + , r));
 }

 int main() {
     scanf("%d%d%d", &n, &c, &d);
     mx1 = -, mx2 = -;
     for(int i = ; i <= n; i++) {
         scanf("%d%d%s", &bea, &cost, op);
         if(op[] == 'C') {
             if(cost <= c && bea > mx1) {
                 mx1 = bea;
             }
             num1[++t1] = node(bea, cost);
         } else {
             if(cost <= d && bea > mx2) {
                 mx2 = bea;
             }
             num2[++t2] = node(bea, cost);
         }
     }
     int ans = ;
     build(, , maxn); //因为C-num[i].cost可能等于0，所以线段树的区间需要从0开始
     for(int i = ; i <= t1; i++) {
         if(c >= num1[i].cost) {
             int t = query(, , c - num1[i].cost);
             if(t != ) {
                 ans = max(ans, t + num1[i].bea);
             }
         }
         update(, num1[i].cost, num1[i].bea);
     }
     build(, , maxn);
     for(int i = ; i <= t2; i++) {
         if(d >= num2[i].cost) {
             int t = query(, , d - num2[i].cost);
             if(t != ) {
                 ans = max(ans, t + num2[i].bea);
             }
         }
         update(, num2[i].cost, num2[i].bea);
     }
     if(mx1 != - && mx2 != -) { //一个用钻石支付，一个用现金支付
         ans = max(ans, mx1 + mx2);
     }
     printf("%d\n", ans);
     return ;
 }