用 Tarjan 算法求解无向图的割点和割边

上期回顾：https://www.cnblogs.com/ofnoname/p/18823922

Tarjan 算法与无向图

连接性分析是图论的核心，而Tarjan算法为我们提供了穿透复杂网络结构的通用方法。之前，我们深入探讨了Tarjan如何利用深度优先搜索(DFS) 的时间戳(dfn[])和回溯值(low[]) 的概念，高效地识别有向图中的强连通分量(SCC)。这种方法通过维护栈结构和巧妙的时间戳比较，将看似复杂的连通性问题转化为优雅的线性时间解决方案。

现在，当我们从有向图转向无向图领域，一个全新的连通性问题浮出水面：如何识别无向图中的割点(cut vertices) 和割桥(bridges)？

有趣的是，尽管问题领域不同，Tarjan算法展现出了惊人的通用性。在无向图中，DFS遍历同样会生成一棵搜索树，但这里有一个关键差异：由于无向图任两点总是互相可达（连通的话），无向图的DFS树不存在横叉边。当我们在无向图上执行DFS时，所有非树边都必然是连接节点与其祖先的返祖边(back edges)。这一特性简化了连通性分析，使得我们可以继续延用dfn和low这对黄金搭档：

• dfn[u]：节点u的DFS访问时间戳（不变的含义）
• low[u]：记录节点u通过树边和最多一条返祖边能到达的最小时间戳

理解无向图割点不仅具有理论价值，更是许多实际系统的基石。想象一下：当这些关键节点代表网络路由器、电力枢纽或社交网络中的信息桥梁时，识别它们就成为了系统可靠性的第一道防线。这也是网络可靠性分析、社交网络关键人物识别、交通枢纽规划等实际应用中的核心问题。

无向图割点问题

在无向图 \(G=(V,E)\) 中，顶点 u 被称为割点(cut vertex/articulation point)，当且仅当删除 u 及其关联边后，图的连通分量数量增加。

想象一个现实的网络：割点就像关键枢纽站，如果它瘫痪，整个网络会被分割成孤立区域；社交网络中，割点就是那个连接不同社群的关键人物；在计算机网络中，割点相当于核心路由器，一旦故障会导致子网断开连接。

割点的求解

总不可能依次去掉点来验证新图是否连通吧！这是仍需要使用 Tarjan 算法。

1. 初始化：

   • 为每个节点维护两个数组：dfn[u]为DFS访问 u 的时间戳；low[u]为 u 通过树边或一条返祖边能到达的最小时间戳
   • 设置全局计数器timestamp，统计时间戳

2. DFS遍历：进行遍历，按照规则更新时间戳和可达的最小时间戳数组。

def dfs(u, parent):
   初始化 dfn[u] = low[u]
   child_count = 0

   for v in neighbors(u):
       if v == parent: continue  # 关键：跳过父节点

       if not visited[v]:
           child_count += 1
           dfs(v, u)
           low[u] = min(low[u], low[v])  # 更新回溯值

           # 割点判断条件
           if (u不是根 and low[v] >= dfn[u]) or
              (u是根 and child_count >= 2):
               mark u as cut vertex
       else:
           low[u] = min(low[u], dfn[v])  # 处理返祖边

1. 割点判断条件：
   • 根节点：当且仅当在DFS树中有≥2个子树
   • 非根节点：当且仅当存在子节点v满足low[v] >= dfn[u]

正确性证明

为什么low[v] >= dfn[u]能检测割点？

按照定义，low[v] >= dfn[u]意味着v的子树无法绕过u访问更早的祖先，删除u后，v的子树将与其他部分断开。反证：若存在其他路径，则low[v]应小于dfn[u]

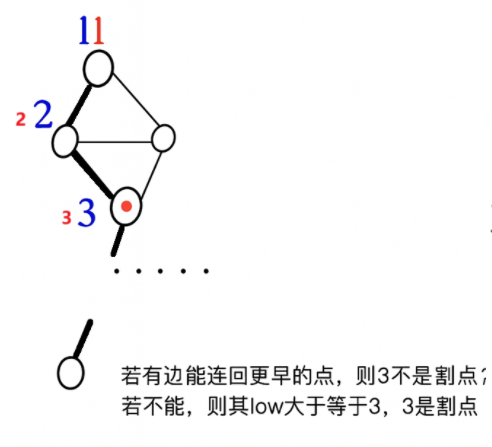
而根节点比较特殊，因为其在搜索树中没有父节点了。只要他有大于1个子树，删除根节点就会让子树分开，所以根节点是割点。

class Graph {
    vector<vector<int>> edges;  // 邻接表
    int n;                     // 顶点数
    int time = 0;              // 全局时间戳
    vector<int> disc;          // 发现时间(dfn)
    vector<int> low;           // 回溯值
    vector<bool> isCut;        // 记录割点
    vector<int> parent;        // 父节点数组

    void dfs(int u) {
        disc[u] = low[u] = ++time;
        int children = 0;  // 记录子树数量

        for (int v : edges[u]) {
            // 跳过父节点
            if (v == parent[u]) continue;

            if (disc[v] == 0) {  // 未访问
                parent[v] = u;
                children++;
                dfs(v);

                // 更新当前节点的low值
                low[u] = min(low[u], low[v]);

                // 非根节点割点判断
                if (parent[u] != -1 && low[v] >= disc[u]) {
                    isCut[u] = true;
                }
            }
            // 处理返祖边
            else {
                low[u] = min(low[u], disc[v]);
            }
        }

        // 根节点特殊判断
        if (parent[u] == -1 && children >= 2) {
            isCut[u] = true;
        }
    }

public:
    Graph(int n) : n(n), edges(n), disc(n, 0), low(n, 0),
                  isCut(n, false), parent(n, -1) {}

    // 无向图添加双向边
    void addEdge(int u, int v) {
        edges[u].push_back(v);
        edges[v].push_back(u);
    }

    // 寻找所有割点
    vector<int> findCutVertices() {
        for (int i = 0; i < n; ++i) {
            if (disc[i] == 0) {
                parent[i] = -1;  // 标记为根
                dfs(i);
            }
        }

        vector<int> result;
        for (int i = 0; i < n; ++i) {
            if (isCut[i]) result.push_back(i);
        }
        return result;
    }

    void printCutVertices() const {
        cout << "Cut Vertices: ";
        for (int i = 0; i < n; ++i) {
            if (isCut[i]) cout << i << " ";
        }
        cout << endl;
    }
};

复杂度分析

• 时间复杂度： $O(V+E) $。DFS 里每个节点和边只访问一次
• 空间复杂度：\(O(V)\) 存储disc、low、parent等数组

无向图割边问题

在无向图 \(G=(V,E)\) 中，边 \(e=(u,v)\) 被称为割边(bridge)或桥，当且仅当删除该边后，图的连通分量数量增加。割边如同连接岛屿的最后一座桥梁，一旦断裂，陆地便永远分离。

与割点的关键区别在于，我们仅删除单一边。割点可能影响多个连通分量，割边必定只影响两个连通分量。

割边的求解

在无重边的无向图中，割边检测只需对割点算法做一处关键修改：

// 割点判断条件
if (low[v] >= dfn[u]) → 割点

// 割边判断条件
if (low[v] > dfn[u]) → 边(u,v)是割边

为什么条件更严格？

• low[v] >= dfn[u] 意味着v的子树无法绕过u
• low[v] > dfn[u] 意味着v的子树甚至无法到达u本身

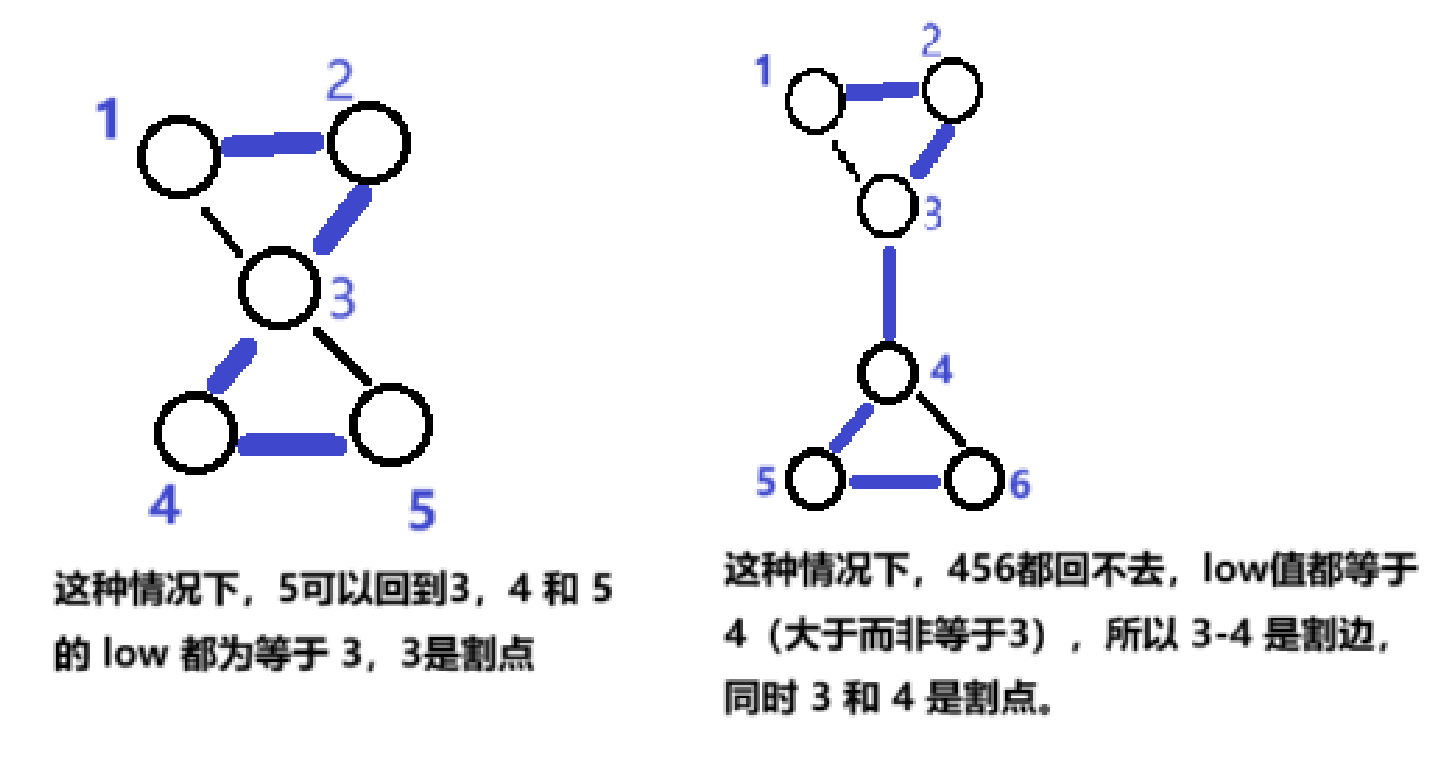
几何解释：

设 u 是 v 的父节点，边 (u,v) 为树边：

• 若存在返祖边使low[v] = dfn[u]，则v的子树能直接连回u
• 若low[v] > dfn[u]，则v的子树只能到达比u更晚的节点
• 删除 (u,v) 后，v 的子树与 u 的连通性被完全破坏

class Graph {
    // ...
    vector<pair<int, int>> bridges;  // 新增：存储割边

    void dfs(int u) {
        // ...
            if (disc[v] == 0) {  // 未访问节点
                // ...
                // 割边判断（关键修改：> 而非 >=）
                if (low[v] > disc[u]) {
                    bridges.push_back({min(u, v), max(u, v)});  // 避免重复
                }
            }
            else {  // 已访问节点（返祖边）
                low[u] = min(low[u], disc[v]);
            }
        }

        // 根节点割点判断
        if (parent[u] == -1 && children >= 2) {
            isCut[u] = true;
        }
    }

public:
    Graph(int n) : n(n), edges(n), disc(n, 0), low(n, 0),
                  parent(n, -1), isCut(n, false) {}

    void addEdge(int u, int v) {
        edges[u].push_back(v);
        edges[v].push_back(u);
    }

    // 返回割点列表
    vector<int> getCutVertices() {
        // 初始化
        fill(disc.begin(), disc.end(), 0);
        fill(low.begin(), low.end(), 0);
        fill(parent.begin(), parent.end(), -1);
        fill(isCut.begin(), isCut.end(), false);
        bridges.clear();
        time = 0;

        for (int i = 0; i < n; ++i) {
            if (disc[i] == 0) dfs(i);
        }

        vector<int> result;
        for (int i = 0; i < n; ++i) {
            if (isCut[i]) result.push_back(i);
        }
        return result;
    }

    // 返回割边列表（按字典序排序）
    vector<pair<int, int>> getBridges() {
        getCutVertices();  // 计算同时获取割点和割边
        sort(bridges.begin(), bridges.end());  // 排序保证输出一致
        return bridges;
    }

    void printBridges() {
        auto res = getBridges();
        cout << "Bridges:\n";
        for (auto [u, v] : res) {
            cout << u << " - " << v << endl;
        }
    }
};

有重边情况的处理

有一个问题在于，上述实现假设图中不存在重边（即任意两节点间最多一条边）。当存在重边时，原推论显然不再正确。若节点 u 和 v 间有 k 条重边，则他们都不可能是割边（删除一条还有其他连接），需要再稍作修改。

处理重边的关键在于区分普通树边与返祖边(重边中的非树边应视为有效的返祖边)。当一个节点到其父亲有多于一条边时，我们就允许其通过多余的边返回父亲，将其视为一般的返祖边。

for (int v : edges[u]) {
    // 原始跳过：if (v == parent[u]) continue;

    // 重边适应：允许通过父节点的重边更新low
    if (v == parent[u]) {
        if (edgeCount[u][v] > 1) {  // 存在重边
            low[u] = min(low[u], disc[v]);  // 视为返祖边
        }
        continue;
    }
    // ...其余逻辑不变
}

if (low[v] > disc[u]) {
    if (edgeCount[u][v] == 1) {  // 必须是单边
        bridges.push_back({u, v});
    }
}