【Linux】【Services】【KVM】安装与简单配置

1. 环境:

1.1. OS: Red Hat Enterprise Linux Server release 7.4 (Maipo)

1.2. Kernel: 3.10.0-693.el7.x86_64

2.安装:

2.1. 操作系统安装：

2.2. 打开VT-x/AMD-V功能：

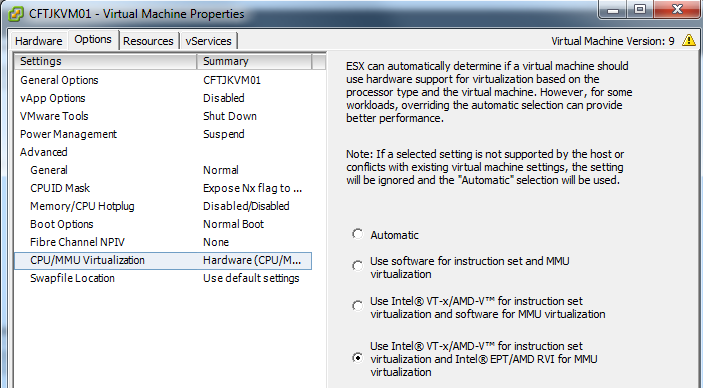
我在ESXi上创建的虚拟机，打开位置见下图，默认是Automatic

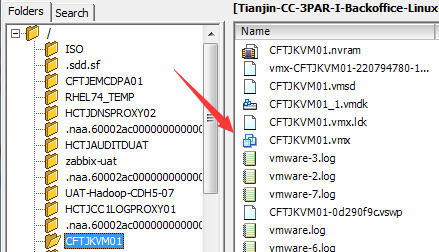
打开虚拟机在ESXi上存储的位置

找到机器名字.vmx文件

在最后一行添加

vhv.enable = "TRUE"

这个操作需要把文件先下载到本地再编辑，完成后上传回去，如果有CLI，可是直接登录到ESXi的SSH上修改

确认CPU已经支持虚拟化

2.3 我使用光盘镜像groupinstall的

#如果刚学习KVM，可以使用virt-manager图形管理工具体验一下
#但是我使用的是xmanager，如果不安装图形界面是无法正常显示到桌面的
yum -y groupinstall "Virtualization Host" "Server with GUI"
yum install virt-viewer qemu-kvm-tools virt-install virt-manager libguestfs-tools 

2.4 执行 virt-manager弹出界面

3. 配置

3.1. 网络配置

禁用NetworkManager服务

systemctl stop NetworkManager && systemctl disable NetworkManager

我在机器上配置了两块网卡，一块用来登录机器和管理，一块用来做桥接的网卡，分别是ens192和ens224

修改/etc/sysconfig/network-scripts/ifcfg-ens192，记得关闭IPV6和NM_CONTROL

TYPE="Ethernet"
PROXY_METHOD="none"
BROWSER_ONLY="no"
BOOTPROTO="none"
DEFROUTE="yes"
IPV4_FAILURE_FATAL="no"
NAME="ens192"
DEVICE="ens192"
ONBOOT="yes"
IPADDR="10.30.2.21"
PREFIX="24"
GATEWAY="10.30.2.254"

ifcfg-ens224

TYPE="Ethernet"
PROXY_METHOD="none"
BROWSER_ONLY="no"
BOOTPROTO="none"
DEFROUTE="yes"
IPV4_FAILURE_FATAL="no"
NAME="ens224"
DEVICE="ens224"
ONBOOT="yes"
#IPADDR="10.30.2.121"
#PREFIX="24"
#GATEWAY="10.30.2.254"
BRIDGE=br0

ifcfg-br0

TYPE="Bridge"
PROXY_METHOD="none"
BROWSER_ONLY="no"
BOOTPROTO="static"
DEFROUTE="yes"
IPV4_FAILURE_FATAL="no"
NAME="br0"
DEVICE="br0"
ONBOOT="yes"
IPADDR="10.30.2.121"
PREFIX="24"
GATEWAY="10.30.2.254"
USECTL="no"

重启网络

systemctl restart network

3.2. KVM配置