YAPTCHA(hdu2973)

YAPTCHA

Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 862    Accepted Submission(s): 452

Problem Description

The
math department has been having problems lately. Due to immense amount
of unsolicited automated programs which were crawling across their
pages, they decided to put
Yet-Another-Public-Turing-Test-to-Tell-Computers-and-Humans-Apart on
their webpages. In short, to get access to their scientific papers, one
have to prove yourself eligible and worthy, i.e. solve a mathematic
riddle.

However, the test turned out difficult for some math
PhD students and even for some professors. Therefore, the math
department wants to write a helper program which solves this task (it is
not irrational, as they are going to make money on selling the
program).

The task that is presented to anyone visiting the start page of the math department is as follows: given a natural n, compute

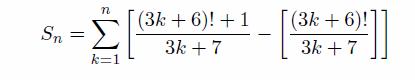
where [x] denotes the largest integer not greater than x.

 

Input

The
first line contains the number of queries t (t <= 10^6). Each query
consist of one natural number n (1 <= n <= 10^6).

 

Output

For each n given in the input output the value of Sn.

 

Sample Input

13
1
2
3
4
5
6
7
8
9
10
100
1000
10000

 

Sample Output

0
1
1
2
2
2
2
3
3
4
28
207
1609

思路：素数打表+威尔逊定理；

 1 #include<stdio.h>
 2 #include<algorithm>
 3 #include<iostream>
 4 #include<string.h>
 5 #include<queue>
 6 #include<set>
 7 #include<math.h>
 8 using namespace std;
 9 typedef long long LL;
10 bool prime[4000000];
11 int sum[4000009];
12 int main(void)
13 {
14         int n;
15         memset(prime,0,sizeof(prime));
16         for(int i = 2; i < 3000; i++)
17         {
18                 if(!prime[i])
19                         for(int j = i; (i*j) <=4000007 ; j++)
20                         {
21                                 prime[i*j] = true;
22                         }
23         }
24         memset(sum,0,sizeof(sum));
25         for(int i = 1; i <= 1000000; i++)
26         {
27                 if(!prime[3*i+7])
28                         sum[i] = sum[i-1] + 1;
29                 else sum[i] = sum[i-1];
30         }
31         scanf("%d",&n);
32         while(n--)
33         {
34                 int ask ;
35                 scanf("%d",&ask);
36                 printf("%d\n",sum[ask]);
37         }
38         return 0;
39 }