AGC036 A-Triangle | 构造

题目链接

题意：

给出一个数$S(1\leqslant S \leqslant 10^{18})$。

要求在平面直角坐标系中找到三个点$(X_1,Y_1),(X_2,Y_2),(X_3,Y_3)$，满足$0\leqslant X_1,Y_1,X_2,Y_2,X_3,Y_3 \leqslant 10^9$且以这三个点为顶点的三角形的面积等于$\dfrac{S}{2}$。输出任意一种方案。

题解：

比赛时做这题做到自闭。

考虑令$(X_1,Y_1)$为$(0,0)$，那么最后形成的三角形就会类似于下面这样子。

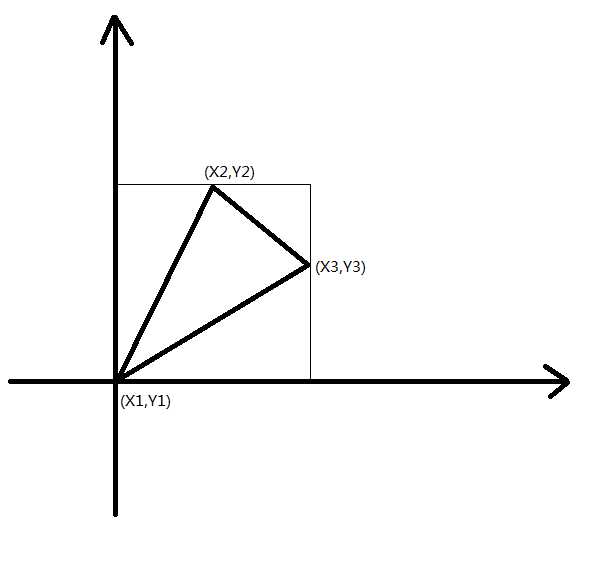
如图，用矩形面积减去周围三个三角形面积可得所求三角形面积为$\dfrac{1}{2}  X_3 Y_2 - \dfrac{1}{2} X_2 Y_3$。

那么我们就要使得$\dfrac{1}{2} X_3 Y_2 - \dfrac{1}{2} X_2 Y_3 = \dfrac{S}{2}$，即$X_3 Y_2 - X_2 Y_3 = S$。

考虑令$(X_2,Y_2)$为$(1,10^9)$，那么就有$10^9 X_3  - Y_3 = S$。

由于坐标均为非负数，所以一定有$10^9 X_3 \geqslant S$，那$-Y_3$可以看成是在减去$10^9 X_3$比$S$多出来的部分。

所以我们只要找到一个最小的$X_3$，使得$10^9 X_3 \geqslant S$，再使$Y_3=10^9 X_3 - S$即可。

这样子处理，求出来的$X_3$和$Y_3$一定是小于等于$10^9$的。

然后我们就做完了。

#include<iostream>
#include<cstdio>
    using namespace std;
    const long long k=1e9;
int main()
{
    long long S=0;
    scanf("%lld",&S);
    long long x1=0,y1=0;
    long long x2=1,y2=k;
    long long x3=S/k+(S%k!=0),y3=x3*k-S;
    printf("%lld %lld %lld %lld %lld %lld",x1,y1,x2,y2,x3,y3);
    return 0;
}

AGC036 A

做题时思维要发散，可以先猜想一些结论，然后再去慢慢验证，最后得出正解。