矩阵快速幂（以HDU1757为例）

对于数据量大的求余运算，在有递推式的情况下，可以构造矩阵求解。

A - A Simple Math Problem

Lele now is thinking about a simple function f(x).

If x < 10 f(x) = x. 
If x >= 10 f(x) = a0 * f(x-1) + a1 * f(x-2) + a2 * f(x-3) + …… + a9 * f(x-10); 
And ai(0<=i<=9) can only be 0 or 1 .

Now, I will give a0 ~ a9 and two positive integers k and m ,and could you help Lele to caculate f(k)%m.

InputThe problem contains mutiple test cases.Please process to the end of file. 
In each case, there will be two lines. 
In the first line , there are two positive integers k and m. ( k<2*10^9 , m < 10^5 )
In the second line , there are ten integers represent a0 ~ a9. 
OutputFor each case, output f(k) % m in one line.Sample Input

10 9999
1 1 1 1 1 1 1 1 1 1
20 500
1 0 1 0 1 0 1 0 1 0

Sample Output

45
104

对于以上题目，已经给出递推式，可以获得如下矩阵：

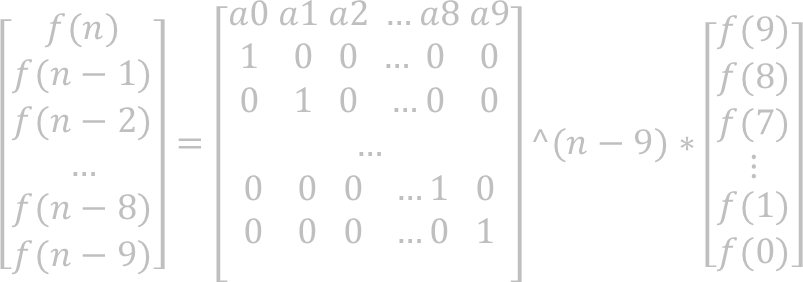
因而只需要用矩阵快速幂求出第一行所得结果对题中所给数据求余的结果即是答案。

首先定义矩阵结构体，并且重载运算符*：

struct Matrix
{
    long long  mat[maxn][maxn];
    Matrix operator*(const Matrix& m)const///重载*运算符，使其能进行矩阵相乘的运算
    {
        Matrix tmp;
        for(int i =  ; i < maxn ; i++)
        {
            for(int j =  ; j < maxn ; j++)
            {
                tmp.mat[i][j] = ;
                for(int k =  ; k < maxn ; k++)
                {
                    tmp.mat[i][j] += mat[i][k]*m.mat[k][j]%mod;
                    tmp.mat[i][j] %= mod;
                }
            }
        }
        return tmp;
    }
};

以下是矩阵快速幂函数：

long long Fast_Matrax(Matrix &m , int k)
{
    Matrix ans;
    memset(ans.mat ,  , sizeof(ans.mat));
    for(int i =  ; i < maxn ; i++)
        ans.mat[i][i] = ;///对角线上的数应该都为1
    k -= ;///递推公式中有9个子项
    while(k)///进行矩阵的快速幂运算
    {
        if(k&)
            ans = ans*m;
        k >>= ;///相当于k/=2
        m = m*m;
    }
    long long sum = ;
    for(int i =  ; i < maxn ; i++)///由于矩阵快速幂之后要与对应的子函数相乘然后进行相加求和，其中
    {
        sum += ans.mat[][i]*f[maxn-i-]%mod;
        sum %= mod;///需要注意这里的一条定理，每个数除以x的余数之和等于它们的和的除以x的余数
    }
    return sum;
}

解本题的完整代码如下：

#include<cstdio>
#include<cstring>
using namespace std;

const int maxn=;
long long k,mod;
int a[maxn],f[maxn];

struct Matrix
{
    long long  mat[maxn][maxn];
    Matrix operator*(const Matrix& m)const///重载*运算符，使其能进行矩阵相乘的运算
    {
        Matrix tmp;
        for(int i =  ; i < maxn ; i++)
        {
            for(int j =  ; j < maxn ; j++)
            {
                tmp.mat[i][j] = ;
                for(int k =  ; k < maxn ; k++)
                {
                    tmp.mat[i][j] += mat[i][k]*m.mat[k][j]%mod;
                    tmp.mat[i][j] %= mod;
                }
            }
        }
        return tmp;
    }
};

void init(Matrix &m)
{
    memset(m.mat ,  , sizeof(m.mat));
    for(int i =  ; i < maxn ; i++)
        m.mat[][i] = a[i];
    for(int i =  ; i < maxn - ; i++)
        m.mat[i+][i] = ;
    for(int i =  ; i < maxn ; i++)
        f[i] = i;
}

long long Fast_Matrax(Matrix &m , int k)
{
    Matrix ans;
    memset(ans.mat ,  , sizeof(ans.mat));
    for(int i =  ; i < maxn ; i++)
        ans.mat[i][i] = ;///对角线上的数应该都为1
    k -= ;///递推公式中有9个子项
    while(k)///进行矩阵的快速幂运算
    {
        if(k&)
            ans = ans*m;
        k >>= ;///相当于k/=2
        m = m*m;
    }
    long long sum = ;
    for(int i =  ; i < maxn ; i++)///由于矩阵快速幂之后要与对应的子函数相乘然后进行相加求和，其中
    {
        sum += ans.mat[][i]*f[maxn-i-]%mod;
        sum %= mod;///需要注意这里的一条定理，每个数除以x的余数之和等于它们的和的除以x的余数
    }
    return sum;
}

int main()
{
    Matrix m;
    while(~scanf("%lld%lld",&k,&mod))
    {
        for(int i=; i<; i++)
            scanf("%d",&a[i]);
            init(m);
        if(k<)
            printf("%d\n",k%mod);
        else
            printf("%lld\n",Fast_Matrax(m,k));
    }
    return ;
}

其中快速幂算法如下：

int PowerMod(int a, int b, int c)///a为底数，b为幂数，c为要除以的数，有时需要使用long long类型
{
    int ans = ;
    a = a % c;
    while(b)
    {
        if(b&)///位运算，判断是否为奇数
            ans = (ans * a) % c;
        b >>=;///等价于b/=2
        a = (a * a) % c;
    }
    return ans;
}

矩阵快速幂即是将上述算法中的正整数换成矩阵进行相乘，然后取矩阵第一行进行函数求和取余。需要注意的是在本题中重载预算符时已经对矩阵中的数进行了求余运算，因此保证了矩阵中的数在一定范围内，并且之后需要进行递推公式中的函数求和，在求和的过程中可以直接取余相加。