bzoj 1093 最大半连通子图 - Tarjan - 拓扑排序 - 动态规划

一个有向图G=(V,E)称为半连通的(Semi-Connected)，如果满足：?u,v∈V，满足u→v或v→u，即对于图中任意两点u，v,存在一条u到v的有向路径或者从v到u的有向路径。若G'=(V',E')满足V'?V，E'是E中所有跟V'有关的边，则称G'是G的一个导出子图。若G'是G的导出子图，且G'半连通，则称G'为G的半连通子图。若G'是G所有半连通子图中包含节点数最多的，则称G'是G的最大半连通子图。给定一个有向图G，请求出G的最大半连通子图拥有的节点数K，以及不同的最大半连通子图的数目C。由于C可能比较大，仅要求输出C对X的余数。

Input

　　第一行包含两个整数N，M，X。N，M分别表示图G的点数与边数，X的意义如上文所述接下来M行，每行两个正整数a, b，表示一条有向边(a, b)。图中的每个点将编号为1,2,3…N，保证输入中同一个(a,b)不会出现两次。N ≤100000, M ≤1000000；对于100%的数据， X ≤10^8

Output

　　应包含两行，第一行包含一个整数K。第二行包含整数C Mod X.

Sample Input

6 6 20070603
1 2
2 1
1 3
2 4
5 6
6 4

Sample Output

3
3

---

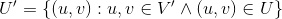　　题目大意 一个有向图G(V, U)是半连通的，当且仅当任意点，并且存在一条路径，它上面的所有边属于U，并且从u到v或者从v到u。图G的导出子图G‘(V'. U')，满足.一个有向图G的半连通子图是一个导出子图且半连通，最大半连通子图是其中拥有最多点数的半连通子图。问最大的半连通子图的点数和数量。

　　因为半连通子图一定是导出子图，所以两个半连通子图是否同构之和它们的定点集合有关。

　　由于图上可能有环(强连通分量)，所以考虑缩点。缩点后的图是个DAG，然后你可得到一个结论就是这个DAG上的一条路径就是原图的一个半连通子图，并且DAG上的路径和原图中的半连通子图一一对应。

　　我们可以赋予每个点一个点权，代表它在原图中代表的点数。

　　于是这个问题转换成在DAG上最长路及其计数。这个拓扑排序再加个小dp就可以水过了。

　　另外注意拓扑排序的时判断重边。

Code

 /**
  * bzoj
  * Problem#1093
  * Accepted
  * Time: 1988ms
  * Memory: 13740k
  */
 #include <bits/stdc++.h>
 using namespace std;
 typedef bool boolean;
 #define smin(a, b) a = min(a, b)
 #define smax(a, b) b = max(a, b)

 int n, m;
 int moder;
 vector<int> *g;

 inline void init() {
     scanf("%d%d%d", &n, &m, &moder);
     g = new vector<int>[(n + )];
     for(int i = , u, v; i <= m; i++) {
         scanf("%d%d", &u, &v);
         g[u].push_back(v);
     }
 }

 int cnt = ;
 stack<int> s;
 int* visitID;
 int* exitID;
 int* belong;
 boolean *visited;
 boolean *instack;
 inline void init_tarjan() {
     visitID = new int[(n + )];
     exitID = new int[(n + )];
     visited = new boolean[(n + )];
     instack = new boolean[(n + )];
     belong = new int[(n + )];
     memset(visited, false, sizeof(boolean) * (n + ));
     memset(instack, false, sizeof(boolean) * (n + ));
 }

 void tarjan(int node) {
     visitID[node] = exitID[node] = ++cnt;
     visited[node] = instack[node] = true;
     s.push(node);

     for(int i = ; i < (signed)g[node].size(); i++) {
         int& e = g[node][i];
         if(!visited[e]) {
             tarjan(e);
             smin(exitID[node], exitID[e]);
         } else if(instack[e]) {
             smin(exitID[node], visitID[e]);
         }
     }

     if(visitID[node] == exitID[node]) {
         int e;
         do {
             e = s.top();
             s.pop();
             instack[e] = false;
             belong[e] = node;
         } while(e != node);
     }
 }

 vector<int> *ng;
 int* dag;
 int *val;
 inline void rebuild() {
     dag = new int[(n + )];
     ng = new vector<int>[(n + )];
     val = new int[(n + )];
     memset(val, , sizeof(int) * (n + ));
     memset(dag, , sizeof(int) * (n + ));

     for(int i = ; i <= n; i++)
         for(int j = ; j < (signed)g[i].size(); j++) {
             int& e = g[i][j];
             if(belong[e] != belong[i])
                 ng[belong[i]].push_back(belong[e]), dag[belong[e]]++;
         }

     for(int i = ; i <= n; i++)
         val[belong[i]]++;
 }

 queue<int> que;
 int *dis;
 int *counter;
 inline void topu() {
     dis = new int[(n + )];
     counter = new int[(n + )];
     memset(dis, , sizeof(int) * (n + ));
     memset(visited, false, sizeof(boolean) * (n + ));

     for(int i = ; i <= n; i++)
         if(belong[i] == i && !dag[i])
             que.push(i), dis[i] = val[i], counter[i] = ;

     while(!que.empty()) {
         int e = que.front();
         que.pop();
         for(int i = ; i < (signed)ng[e].size(); i++) {
             int& eu = ng[e][i];
             dag[eu]--;
             if(!dag[eu])
                 que.push(eu);
             if(visited[eu])    continue;
             visited[eu] = true;

             if(dis[e] + val[eu] > dis[eu]) {
                 dis[eu] = dis[e] + val[eu];
                 counter[eu] = counter[e];
             } else if(dis[e] + val[eu] == dis[eu])
                 counter[eu] = (counter[eu] + counter[e]) % moder;
         }
         for(int i = ; i < (signed)ng[e].size(); i++)
             visited[ng[e][i]] = false;
     }
 }

 int maxdis = -, res = ;
 inline void solve() {
     for(int i = ; i <= n; i++) {
         if(belong[i] != i)    continue;
         if(dis[i] > maxdis)    {
             maxdis = dis[i];
             res = counter[i];
         } else if(dis[i] == maxdis)
             (res += counter[i]) %= moder;
     }
     printf("%d\n%d", maxdis, res);
 }

 int main() {
     init();
     init_tarjan();
     for(int i = ; i <= n; i++)
         if(!visited[i])
             tarjan(i);
     rebuild();
     topu();
     solve();
     return ;
 }