PCA-主成分分析(Principal components analysis)
来自:刘建平
主成分分析(Principal components analysis,以下简称PCA)是最重要的降维方法之一。
1. PCA的思想
PCA顾名思义,就是找出数据里最主要的方面,用数据里最主要的方面来代替原始数据。
我们降维的标准为:样本点到这个超平面的距离足够近,或者说样本点在这个超平面上的投影能尽可能的分开。
基于上面的两种标准,我们得到PCA的两种等价推导。
2. PCA的推导:基于最小投影距离
第一种:样本点到这个超平面的距离足够近。
假设m个n维数据  都已经进行了中心化,即
都已经进行了中心化,即 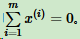 经过投影变换得到新坐标系为
经过投影变换得到新坐标系为  ,其中w为标准正交基,即
,其中w为标准正交基,即 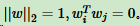
如果我们将数据从n维降到n'维,即丢弃新坐标系中的部分坐标,则新的坐标系为  ,样本点 x(i) 在 n' 维坐标系中的投影为:
,样本点 x(i) 在 n' 维坐标系中的投影为: 其中,
其中,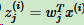 是x(i)在低维坐标系里第 j 维的坐标。
是x(i)在低维坐标系里第 j 维的坐标。
如果我们用 z(i) 来恢复原始数据 x(i) ,则得到的恢复数据 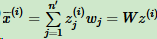 ,其中,w为标准正交基组成的矩阵。
,其中,w为标准正交基组成的矩阵。
现在考虑整个样本集,我们希望所有的样本到这个超平面的距离足够近,即最小化式:
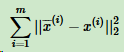
将这个式子整理:
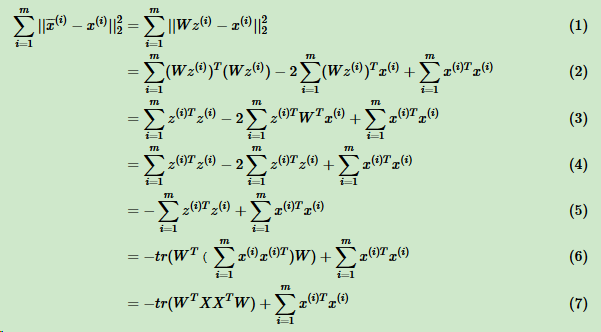
PCA-主成分分析(Principal components analysis)的更多相关文章
- 主成分分析 | Principal Components Analysis | PCA
理论 仅仅使用基本的线性代数知识,就可以推导出一种简单的机器学习算法,主成分分析(Principal Components Analysis, PCA). 假设有 $m$ 个点的集合:$\left\{ ...
- 【机器学习】主成分分析PCA(Principal components analysis)
1. 问题 真实的训练数据总是存在各种各样的问题: 1. 比如拿到一个汽车的样本,里面既有以“千米/每小时”度量的最大速度特征,也有“英里/小时”的最大速度特征,显然这两个特征有一个多余. 2. 拿到 ...
- 主成分分析(principal components analysis)
http://www.cnblogs.com/jerrylead/tag/Machine%20Learning/ PCA的思想是将n维特征映射到k维上(k<n),这k维是全新的正交特征.这k维特 ...
- 主成分分析(principal components analysis, PCA)
原理 计算方法 主要性质 有关统计量 主成分个数的选取 ------------------------------------------------------------------------ ...
- A tutorial on Principal Components Analysis | 主成分分析(PCA)教程
A tutorial on Principal Components Analysis 原著:Lindsay I Smith, A tutorial on Principal Components A ...
- [zz] Principal Components Analysis (PCA) 主成分分析
我理解PCA应该分为2个过程:1.求出降维矩阵:2.利用得到的降维矩阵,对数据/特征做降维. 这里分成了两篇博客,来做总结. http://matlabdatamining.blogspot.com/ ...
- Andrew Ng机器学习公开课笔记–Principal Components Analysis (PCA)
网易公开课,第14, 15课 notes,10 之前谈到的factor analysis,用EM算法找到潜在的因子变量,以达到降维的目的 这里介绍的是另外一种降维的方法,Principal Compo ...
- Stat2—主成分分析(Principal components analysis)
最近在猛撸<R in nutshell>这本课,统计部分涉及的第一个分析数据的方法便是PCA!因此,今天打算好好梳理一下,涉及主城分析法的理论以及R实现!come on…gogogo… 首 ...
- Jordan Lecture Note-9: Principal Components Analysis (PCA).
Principal Components Analysis (一)引入PCA 当我们对某个系统或指标进行研究时往往会发现,影响这些系统和指标的因素或变量的数量非常的多.多变量无疑会为科学研究带来 ...
- (4)主成分分析Principal Component Analysis——PCA
主成分分析Principal Component Analysis 降维除了便于计算,另一个作用就是便于可视化. 主成分分析-->降维--> 方差:描述样本整体分布的疏密,方差越大-> ...
随机推荐
- 监控网卡流量脚本(Python)
#!/usr/bin/env python# coding: utf-8# author: Xiao Guaishou try: import psutilexcept ImportError: ...
- 微信小程序canvas把正方形图片绘制成圆形
wxml代码: <view class="result-page"> <canvas canvas-id='firstCanvas' style='width:1 ...
- 统计py文件中的代码行
希望是输入一个合法的文件夹的路径,然后代码自动读取该文件夹下的每个py结尾的文件内的代码行数,最后汇总一个数,但现在只是有思路,却没时间写,这是能读取同级文件下的某个文件, with open('te ...
- fjwc2019 D6T2 密文(trie+贪心)
#194. 「2019冬令营提高组」密文 设$s[i]$表示前$i$个密文的异或和 容易发现,只要知道$s[0]~s[n](s[0]=0)$就可以知道每一位的值. 转化一下,就变成了在完全图上求最小生 ...
- Cannot resolve reference to bean 'sqlSessionFactory' while setting bean
今天下载公司以前的一个项目,要和现在的项目进行整合,下载一切顺利,但在开发机器上一跑,憋了. 有两种日志,两种报错:一个是cannot resolve reference to bean 'sqlSe ...
- c#简单案例--单位转换器
经过几天学习,写出了一个简单的winform应用程序,贴出源码,以备不时之需. 软件启动后的界面如下图所示: 如图,该程序由6个label.8个comboBox.8个textBox和4个button组 ...
- host元素的属性autoDeploy和reloadable的区别
web.xml文件的修改会触发AutoDeploy,受host节的autoDeploy配置值的影响. class类文件修改会触发Reload操作,受reloadable配置值的影响. 而autoDep ...
- Redhat6.4安装MongoDBv3.6.3
运用后台+配置文件方式启动. 条件 下载mongodb-linux-x86_64-rhel62-3.6.3.tar 官网https://www.mongodb.com/download-center? ...
- Unity3D之主菜单
1.新建一个名为MainMenu的C#脚本,修改编码后拖动到主摄像机,并给主摄像机添加一个AudioSource声音源作为背景音乐.将音乐文件赋值给Audio Clip属性. 2.创建一个Common ...
- 20155201 网络攻防技术 实验九 Web安全基础
20155201 网络攻防技术 实验九 Web安全基础 一.实践内容 本实践的目标理解常用网络攻击技术的基本原理.Webgoat实践下相关实验. 二.报告内容: 1. 基础问题回答 1)SQL注入攻击 ...
