机器学习笔记十三：Ensemble思想(上)

从上面几篇的决策树開始,就能够開始进入到集成学习(ensemble learning)了,与其说集成学习是一种算法,倒不如说集成学习是一种思想.

集成学习的思想也是非常自然非常符合人类直观理解的. 用通俗的不能更通俗的话来说,要是一个机器学习器解决不了问题,那就多训练几个.再把这些学习器结合起来完毕机器学习任务. 能够类比开会,一群人讨论得到的解决的方法一般比一个人拍板的要好.

用过集成学习之后,一般来说,效果都会比某些单一的算法效果要好.所以,无论是为了排名还是为了其它的东西,kaggle等机器学习竞赛一大部分方案都会使用集成学习的,你懂得.

这篇仅仅讲集成学习的主要思想和最常见的学习策略.并不带有太多的理论数学推导,在之后的下篇会增加进来.

一.概述

前面就已经讲到了,集成学习的思想是,我们能够训练非常多个学习器,通过一定的结合策略,终于形成一个强的学习器.形象一点看下图.



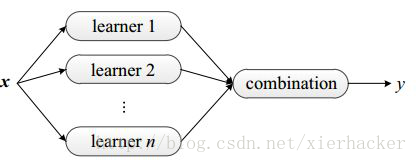
所以,你会非常自然的考虑:

我们通过如何的方式来得到n个学习器呢?

得到n个学习器之后,我们通过如何的策略来结合呢?

以下的内容就这两个疑惑来讲一下常见的训练多个学习器的方法和结合多个学习器的方法.

二.怎么得到多个学习器

这一部分举两个最常见的得到多个学习器的思路.一种是bagging,第二种是boosting.

Ⅰ.bagging

要理解bagging,首先知道bootstrap词汇的故事.这个词汇表示的是靴子上面的小环或者是悬挂物等等,通过这个小东西能够方便穿靴子.意思是不依靠外界的帮助,或者叫做自助法.

在这里表示一种有放回的抽样方法.所以以后看到bootstrap这个词不要不知道是什么意思.相同,你可能会经常看到一个词叫做bootstrap sampling.这个词的意思是自助採样,对于N个样本的训练集,我从里面随机取出m个样本,得到一个子训练集.然后把这些样本放回. 然后再取m个样本,得到第二个子训练集,再放回去………..重复这种步骤k次,得到k个子训练集.

Bagging能够看做是bootstrap aggregation的简写.

bagging得到多个学习器的方式为:

通过自助採样的方法得到K个训练集,然后分别在这K个训练集上面训练学习器.然后就得到了K个学习器.

非常easy的思想,形象一点例如以下图所看到的.

watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQveGllcmhhY2tlcg==/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/SouthEast" alt="这里写图片描写叙述" title="">

须要注意的是,bagging对于弱学习器没有限制,也就是说,你能够用决策树,SVM等等都是能够的.一般经常使用的是决策树和神经网络.

由于baggin的随机採样思路,模型的泛化能力非常强,减少了模型的方差.可是对于训练集的拟合程度就不是那么好,也就是说偏差会大一些.

符合bagging思想的比較出名的学习算法就是随机森林了,在后面会具体来讲随机森林.这里先知道随机森铃的思想算是bagging即可.

Ⅱ.boosting

boosting的思想是:

训练集(当中各个元素)的权重是依据学习器的表现来改变的.

这个和bagging就有非常大的不同了.bagging採用自助採样的方式”产生”出多个训练集.可是boosting仅仅有一个训练集,可是训练集中各个元素(输入向量)的权重是不同的.

具体一点,boosting是先从具有初始权重的训练集训练出一个弱学习器1,然后依据弱学习器1的表现,来更新样本的权重. 然后再具有新的权重的训练集上面训练弱学习器2,然后依据弱学习器2的表现来更新样本的权重……..重复多次 ,得到m个学习器,最后整合这些弱学习器得到强学习器.

形象一点的话看下图.



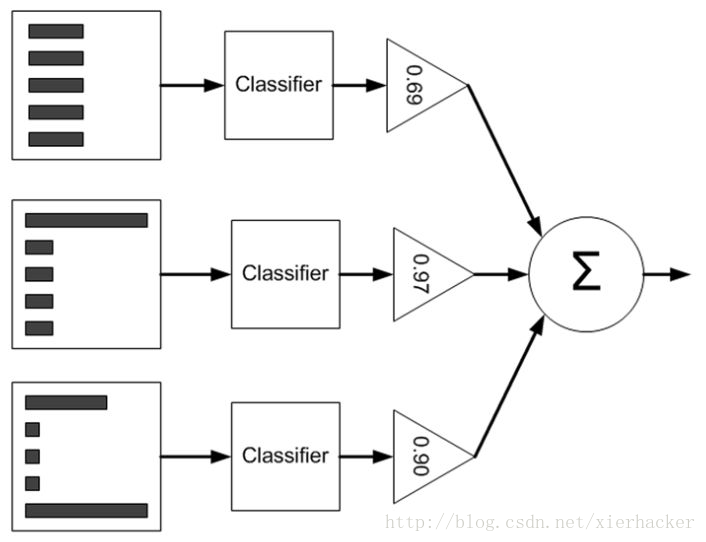
这里并不具体展开讲权重改变的具体细节,由于这篇的目的是高速理解思想,为后面的打基础.更具体的在后面的博客会具体给出.

Boosting框架以下比較出名好用的就是Adaboost算法和提升树了.后面都会讲到.

三.通过如何的策略结合学习器

这里仅仅能说要粗略的带过了,由于后面会从具体的实例里面体会怎么结合各种学习器.比在这里泛泛而谈要实用得多.

重点是要好好理解bagging和boosting的思想.