【转载】 强化学习（四）用蒙特卡罗法（MC）求解

原文地址：

https://www.cnblogs.com/pinard/p/9492980.html

---------------------------------------------------------------------------------------------------

在强化学习（三）用动态规划（DP）求解中，我们讨论了用动态规划来求解强化学习预测问题和控制问题的方法。但是由于动态规划法需要在每一次回溯更新某一个状态的价值时，回溯到该状态的所有可能的后续状态。导致对于复杂问题计算量很大。同时很多时候，我们连环境的状态转化模型P都无法知道，这时动态规划法根本没法使用。这时候我们如何求解强化学习问题呢？本文要讨论的蒙特卡罗(Monte-Calo, MC)就是一种可行的方法。

　　　　蒙特卡罗法这一篇对应Sutton书的第五章和UCL强化学习课程的第四讲部分，第五讲部分。

1. 不基于模型的强化学习问题定义

　　　　在动态规划法中，强化学习的两个问题是这样定义的：

可见, 模型状态转化概率矩阵P始终是已知的，即MDP已知，对于这样的强化学习问题，我们一般称为基于模型的强化学习问题。

　　　　本文要讨论的蒙特卡罗法就是上述  不基于模型 的强化学习问题。

2. 蒙特卡罗法求解特点

　　　　 蒙特卡罗这个词之前的博文也讨论过，尤其是在之前的MCMC系列中。它是一种通过采样近似求解问题的方法。这里的蒙特卡罗法虽然和MCMC不同，但是采样的思路还是一致的。那么如何采样呢？

　　　　蒙特卡罗法通过采样若干经历完整的状态序列(episode)来估计状态的真实价值。所谓的经历完整，就是这个序列必须是达到终点的。比如下棋问题分出输赢，驾车问题成功到达终点或者失败。有了很多组这样经历完整的状态序列，我们就可以来近似的估计状态价值，进而求解预测和控制问题了。

　　　　从特卡罗法法的特点来说，一是和动态规划比，它不需要依赖于模型状态转化概率。二是它从经历过的完整序列学习，完整的经历越多，学习效果越好。

3. 蒙特卡罗法求解强化学习预测问题

这里我们先来讨论蒙特卡罗法求解强化学习控制问题的方法，即策略评估。一个给定策略ππ的完整有T个状态的状态序列如下：

S1,A1,R2,S2,A2,...St,At,Rt+1,...RT,ST

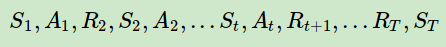
　　　　回忆下强化学习（二）马尔科夫决策过程(MDP)中对于价值函数   ν_π(s)    的定义：  vπ(s)

vπ(s)=Eπ(Gt|St=s)=Eπ(Rt+1+γRt+2+γ2Rt+3+...|St=s)

可以看出每个状态的价值函数等于所有该状态收获的期望，同时这个收获是通过后续的奖励与对应的衰减乘积求和得到。那么对于蒙特卡罗法来说，如果要求某一个状态的状态价值，只需要求出所有的完整序列中该状态出现时候的收获再取平均值即可近似求解，也就是：

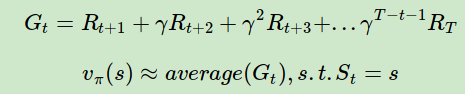
　　　　可以看出，预测问题的求解思路还是很简单的。不过有几个点可以优化考虑。

　　　　第一个点是同样一个状态可能在一个完整的状态序列中重复出现，那么该状态的收获该如何计算？有两种解决方法。第一种是仅把状态序列中第一次出现该状态时的收获值纳入到收获平均值的计算中；另一种是针对一个状态序列中每次出现的该状态，都计算对应的收获值并纳入到收获平均值的计算中。两种方法对应的蒙特卡罗法分别称为：首次访问(first visit) 和每次访问(every visit) 蒙特卡罗法。第二种方法比第一种的计算量要大一些，但是在完整的经历样本序列少的场景下会比第一种方法适用。

　　　　第二个点是累进更新平均值（incremental mean)。在上面预测问题的求解公式里，我们有一个average的公式，意味着要保存所有该状态的收获值之和最后取平均。这样浪费了太多的存储空间。一个较好的方法是在迭代计算收获均值，即每次保存上一轮迭代得到的收获均值与次数，当计算得到当前轮的收获时，即可计算当前轮收获均值和次数。通过下面的公式就很容易理解这个过程：

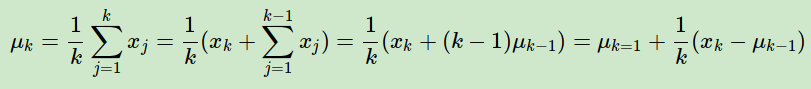
这样上面的状态价值公式就可以改写成：

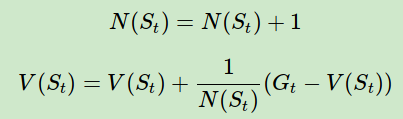
　　　　这样我们无论数据量是多还是少，算法需要的内存基本是固定的 。

　　　　以上就是蒙特卡罗法求解预测问题的整个过程，下面我们来看控制问题求解。

4. 蒙特卡罗法求解强化学习控制问题

在实际求解控制问题时，为了使算法可以收敛，一般ϵ会随着算法的迭代过程逐渐减小，并趋于0。这样在迭代前期，我们鼓励探索，而在后期，由于我们有了足够的探索量，开始趋于保守，以贪婪为主，使算法可以稳定收敛。这样我们可以得到一张和动态规划类似的图：

5. 蒙特卡罗法控制问题算法流程

在这里总结下蒙特卡罗法求解强化学习控制问题的算法流程，这里的算法是在线(on-policy)版本的,相对的算法还有离线(off-policy)版本的。在线和离线的区别我们在后续的文章里面会讲。同时这里我们用的是every-visit,即个状态序列中每次出现的相同状态，都会计算对应的收获值。

　　　　在线蒙特卡罗法求解强化学习控制问题的算法流程如下:

6.  蒙特卡罗法求解强化学习问题小结

　　　　蒙特卡罗法是我们第二个讲到的求解强化问题的方法，也是第一个不基于模型的强化问题求解方法。它可以避免动态规划求解过于复杂，同时还可以不事先知道环境转化模型，因此可以用于海量数据和复杂模型。但是它也有自己的缺点，这就是它每次采样都需要一个完整的状态序列。如果我们没有完整的状态序列，或者很难拿到较多的完整的状态序列，这时候蒙特卡罗法就不太好用了， 也就是说，我们还需要寻找其他的更灵活的不基于模型的强化问题求解方法。

　　　　下一篇我们讨论用时序差分方法来求解强化学习预测和控制问题的方法。

（欢迎转载，转载请注明出处。欢迎沟通交流： liujianping-ok@163.com）

------------------------------------------------------------------------------------------------------------