基于随机游走的三维网格分割算法（Random Walks）

　　首先以一维随机游走（1D Random Walks）为例来介绍下随机游走（Random Walks）算法，如下图所示，从某点出发，随机向左右移动，向左和向右的概率相同，都为1/2，并且到达0点或N点则不能移动，那么如何求该点到达目的地N点的概率。

　　该问题可以描述为如下数学形式：

P(0) = 0

P(N) = 1

P(x) = 1/2*P(x - 1) + 1/2*P(x + 1) for x = 1, 2, 3, … , N-1

　　如果用矩阵形式描述，即：

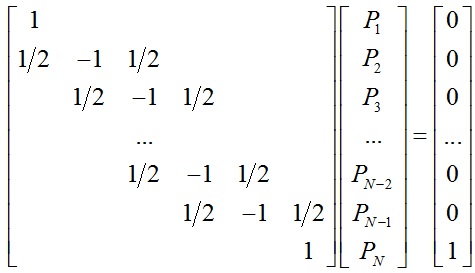
那么通过求解该线性方程组就可以得到各个点到达目的地N点的概率，以上就是一维随机游走算法原理。

[Grady et al. 2006]提出了利用随机游走思想来分割二维图像，文章将图像考虑成一张图（Graph），每个像素对应图中一个节点，根据亮度差值定义节点间的权重（相当于一维随机游走中向左和向右的概率），然后用户指定前景（foreground）和背景（background）标签（相当于一维随机游走中N点和0点），通过求解线性方程组就可以得到各个像素点属于前景或背景的概率，如果将阈值概率设置为0.5，那么就可以分割得到期望的图像区域。

[Lai et al. 2008]将这种思想扩展到三维网格分割，文章将网格中每个三角片对应图中一个节点，利用相邻三角片之间的二面角来定义节点之间的权重，具体如下：

对于三角片f_i，定义一个f_i与相邻三角片f_i,k(k = 1, 2, 3)之间几何差异的函数d(f_i, f_i,k)：

d(f_i, f_i,k) = η·[1 – cos(dihedral(f_i, f_i,k))] = η/2·||N_i – N_i,k||²

其中：dihedral(f_i, f_i,k)代表相邻三角片f_i与f_i,k之间的二面角，N_i为三角片f_i的法向，对于凹边η设置为1.0，对于凸边η设置为0.2。

　　将d归一化：

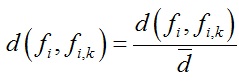
　　节点之间的权重p_i,k可以根据函数d(f_i, f_i,k)给定：

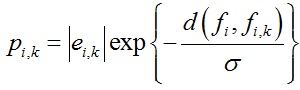
　　同样通过求解线性方程组可以得到网格分割效果。

　　[Zhang et al. 2010]对[Lai et al. 2008]的网格分割算法做了部分改进，文章将网格中每个顶点对应图中一个节点，由于一个网格的三角片数量通常是顶点数量的2倍左右，这样求解的方程变量数就会减少一半左右，计算速度就会得到提高。

效果：

 

本文为原创，转载请注明出处：http://www.cnblogs.com/shushen。

参考文献：

[1] Grady, L., "Random Walks for Image Segmentation," in Pattern Analysis and Machine Intelligence, IEEE Transactions on , vol.28, no.11, pp.1768-1783, Nov. 2006

[2] Yu-Kun Lai, Shi-Min Hu, Ralph R. Martin, and Paul L. Rosin. 2008. Fast mesh segmentation using random walks. In Proceedings of the 2008 ACM symposium on Solid and physical modeling (SPM '08). ACM, New York, NY, USA, 183-191.

[3] Zhang, J., Wu, C., Cai, J., Zheng, J. and Tai, X.-c. (2010), Mesh Snapping: Robust Interactive Mesh Cutting Using Fast Geodesic Curvature Flow. Computer Graphics Forum, 29: 517–526.