CF1249F Maximum Weight Subset

CF1249F Maximum Weight Subset

洛谷评测传送门

题目描述

You are given a tree, which consists of nn vertices. Recall that a tree is a connected undirected graph without cycles.

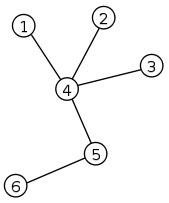Example of a tree.Vertices are numbered from 11 to nn . All vertices have weights, the weight of the vertex vv is a_va**v .

Recall that the distance between two vertices in the tree is the number of edges on a simple path between them.

Your task is to find the subset of vertices with the maximum total weight (the weight of the subset is the sum of weights of all vertices in it) such that there is no pair of vertices with the distance kk or less between them in this subset.

输入格式

The first line of the input contains two integers nn and kk ( 1 \le n, k \le 2001≤n,k≤200 ) — the number of vertices in the tree and the distance restriction, respectively.

The second line of the input contains nn integers a_1, a_2, \dots, a_na1,a2,…,a**n ( 1 \le a_i \le 10^51≤a**i≤105 ), where a_ia**i is the weight of the vertex ii .

The next n - 1n−1 lines contain edges of the tree. Edge ii is denoted by two integers u_iu**i and v_iv**i — the labels of vertices it connects ( 1 \le u_i, v_i \le n1≤u**i,v**i≤n , u_i \ne v_iu**i≠v**i ).

It is guaranteed that the given edges form a tree.

输出格式

Print one integer — the maximum total weight of the subset in which all pairs of vertices have distance more than kk .

题意翻译

给定一棵含nn个节点的树，每个节点含一个点权a[i]a[i]。现在请你选出一些节点，使得这些节点的权值和最大并且这些节点中任意两个节点的距离都>k>k。并输出这个最大的权值。

输入第一行含两个整数n,kn,k，之后是nn个整数a[i]a[i]，之后是n-1n−1行，每行两个整数，描述树的每条边。

输入输出样例

输入 #1复制

输出 #1复制

输入 #2复制

输出 #2复制

题解：

题目翻译过来发第一篇题解（英语巨菜无所谓）

来讲一下正解：树上DP。

我们从0开始为节点编号，并设置0为根节点。

• DP的状态是这样的：设\(dp[x][dep]\)为以\(x\)为根节点的子树中所有选中节点中深度最小的节点深度为\(dep\)时的最大价值（有点绕...请好好理解）

  这里要注意，我们定义的深度并不是整棵树的深度。因为动态规划是利用状态转移，所以我们定义的这个\(dep\)是在当前状态下的深度。通俗地讲，就是这棵子树的深度（子树根节点深度为0）。

那么我们开始考虑状态转移。这道题的一个限定条件（比较难搞）还有一个任意两点的距离都大于\(k\)。我们的状态转移（包括状态设置）都是考虑这个而进行的。

可以看出，对于每一个节点，它既统计了它自己的答案，又对它的合法的祖宗们（滑稽.jpg）的答案有贡献。所以，据此，我们考虑两种情况：第一种，当前的节点是子树的根，这个时候它是它的小家族的最大的祖宗，开始统计它的答案。第二种，当前的节点是儿子或孙儿或...这个时候它要对它上面的祖宗们贡献答案。

根据我们对状态的定义，在第一种情况下，当前节点的深度为0，那么当前节点的答案

\[dp[x][dep]=a[x]+\sum_{to\in children(x)}dp[to][max(0,k-dep)].
\]

在第二种情况下，我们则需要遍历\(x\)节点的所有儿子，然后挑出对答案贡献最大的儿子来更新答案。转移方程就是：

\[dp[x][dep]=max(dp[x][dep],dp[x][dep-1]+\sum_{to\in children(x)}dp[to][max(dep-1,k-dep)]).
\]

这个时候就能比较容易地想到用深搜解决问题。因为深搜的性质恰好满足：从上搜到低，在从低到上更新答案的过程。所以，我们把答案再从\(n-1\)号点跑回\(0\)号点即可。最终的答案就是\(dp[0][0]\)。

代码：

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=210;
int n,k;
int a[maxn],d[maxn],dp[maxn][maxn],tmp[maxn];
int tot,head[maxn],nxt[maxn<<1],to[maxn<<1];
void add(int x,int y)
{
	to[++tot]=y;
	nxt[tot]=head[x];
	head[x]=tot;
}
void dfs(int x,int f)
{
	dp[x][0]=a[x];
	for(int i=head[x];i;i=nxt[i])
	{
		int y=to[i];
		if(y!=f)
			dfs(y,x);
	}
	for(int i=0;i<n;i++)
	{
		if(!i)
		{
			for(int l=head[x];l;l=nxt[l])
			{
				int y=to[l];
				if(y==f)
					continue;
				dp[x][0]+=dp[y][k];
			}
		}
		else
		{
			for(int l=head[x];l;l=nxt[l])
			{
				int y=to[l];
				if(y==f)
					continue;
				int now=dp[y][i-1];
				for(int j=head[x];j;j=nxt[j])
				{
					int yy=to[j];
					if(yy==f || yy==y)
						continue;
					now+=dp[yy][max(i-1,k-i)];
				}
				dp[x][i]=max(dp[x][i],now);
			}
		}
	}
	for(int i=n;i>=1;i--)
		dp[x][i-1]=max(dp[x][i-1],dp[x][i]);
}
int main()
{
	scanf("%d%d",&n,&k);
	for(int i=0;i<n;i++)
		scanf("%d",&a[i]);
	for(int i=0;i<n-1;i++)
	{
		int u,v;
		scanf("%d%d",&u,&v);
		u--,v--;
		add(u,v);
		add(v,u);
	}
	dfs(0,-1);
	printf("%d",dp[0][0]);
	return 0;
}