高德JS依赖分析工程及关键原理

一、背景

高德 App 进行 Bundle 化后，由于业务的复杂性，Bundle 的数量非常多。而这带来了一个新的问题——Bundle 之间的依赖关系错综复杂，需要进行管控，使 Bundle 之间的依赖保持在架构设计之下。

并且，为了保证 Bundle 能实现独立运转，在业务持续迭代的过程中，需要逆向的依赖关系来迅速确定迭代的影响范围。同时，对于切面 API（即对容器提供的系统 API，类似浏览器中的 BOM API），也需要确定每个切面 API 的影响范围以及使用趋势，来作为修改或下线某个 API 的依据。

以组件库为例，由于组件会被若干业务项目所使用，我们对组件的修改会影响这些业务项目。在计划修改前，需要根据正向的依赖关系（业务依赖组件）来算出逆向的依赖关系——该组件被哪些地方所依赖，从而确定这个组件修改的影响范围。

比文件更高的维度，是 Bundle 间的依赖。我们有业务 Bundle，也有公共 Bundle。公共 Bundle 也分为不同层级的 Bundle。

对于公用 Bundle，业务 Bundle 可以依赖它，但公用 Bundle 不能反过来依赖业务 Bundle；同样的，底层的 Bundle 也禁止依赖上层封装的 Bundle。我们需要通过依赖分析，来确保这些依赖按照上述规则进行设计。

二、实现关键步骤

实现 JS 依赖分析，整个实现过程大致如下图所示：

下面挑一些关键步骤来展开介绍。

使用 AST 提取依赖路径

要做文件级别的依赖分析，就需要提取每个文件中的依赖路径，提取依赖路径有 2 个方法：

• 使用正则表达式，优点是方便实现，缺点是难以剔除注释，灵活度也受限；
• 先进行词法分析和语法分析，得到 AST（抽象语法树）后，遍历每个语法树节点，此方案的优点是分析精确，缺点是实现起来要比纯正则麻烦，如果对应语言没有提供 parser API（如 Less），那就不好实现。

一般为了保证准确性，能用第 2 个方案的都会用第 2 个方案。

以类 JS（.js、.jsx、.ts、.tsx）文件为例，我们可以通过 TypeScript 提供的 API ts.createSourceFile 来对类 JS 文件进行词法分析和语法分析，得到 AST：

const ast = ts.createSourceFile(
  abPath,
  content,
  ts.ScriptTarget.Latest,
  false,
  SCRIPT_KIND[path.extname(abPath)]
);

得到 AST 后，就可以开始遍历 AST 找到所有我们需要的依赖路径了。遍历时，可以通过使用 typeScript 模块提供的 ts.forEachChild 来遍历一个语法树节点的所有子节点，从而实现一个遍历函数 walk：

function walk (node: ts.Node) {
  ts.forEachChild(node, walk); // 深度优先遍历

  // 根据不同类型的语法树节点，进行不同的处理
  // 目的是找到 import、require 和 require.resolve 中的路径
  // 上面 3 种写法分为两类——import 声明和函数调用表达式
  // 其中函数调用表达式又分为直接调用（require）和属性调用（require.resolve）
  switch (node.kind) {
    // import 声明处理
    case ts.SyntaxKind.ImportDeclaration:
      // 省略细节……
      break;

    // 函数调用表达式处理
    case ts.SyntaxKind.CallExpression:
      // 省略细节
      break;
  }
}

通过这种方式，我们就可以精确地找到类 JS 文件中所有直接引用的依赖文件了。

当然了，在 case 具体实现中，除了用户显式地写依赖路径的情况，用户还有可能通过变量的方式动态地进行依赖加载，这种情况就需要进行基于上下文的语义分析，使得一些常量可以替换成字符串。

但并不是所有的动态依赖都有办法提取到，比如如果这个动态依赖路径是 Ajax 返回的，那就没有办法了。不过无需过度考虑这些情况，直接写字符串字面量的方式已经能满足绝大多数场景了，之后计划通过流程管控+编译器检验对这类写法进行限制，同时在运行时进行收集报警，要求必需显式引用，以 100% 确保对切面 API 的引用是可以被静态分析的。

建立文件地图进行寻路

我们对于依赖路径的写法，有一套自己的规则：

引用类 JS 文件支持不写扩展名；

引用本 Bundle 文件，可直接只写文件名；

使用相对路径；

引用公用 Bundle 文件，通过 @${bundleName}/${fileName} 的方式引用，fileName 同样是直接只写该 Bundle 内的文件名。

这些方式要比 CommonJS 或 ECMAScript Module 的规划要稍复杂一些，尤其是「直接只写文件名」这个规则。对于我们来说，需要找到这个文件对应的真实路径，才能继续进行依赖分析。

要实现这个，做法是先构建一个文件地图，其数据结构为 { [fileName]: ‘relative/path/to/file’ } 。我使用了 glob 来得到整个 Bundle 目录下的所有文件树节点，筛选出所有文件节点，将文件名作为 key，相对于 Bundle 根目录的路径作为 value，生成文件地图。在使用时，「直接只写文件名」的情况就可以直接根据文件名以 O(1) 的时间复杂度找到对应的相对路径。

此外，对于「引用类 JS 文件支持不写扩展名」这个规则，需要遍历每个可能的扩展名，对路径进行补充后查找对应路径，复杂度会高一些。

依赖是图的关系，需先建节点后建关系

在最开始实现依赖关系时，由于作为前端的惯性思维，会认为「一个文件依赖另一些文件」是一个树的关系，在数据结构上就会自然地使用类似文件树中 children: Node[] 的方式——链式树结构。而实际上，依赖是会出现这种情况的：

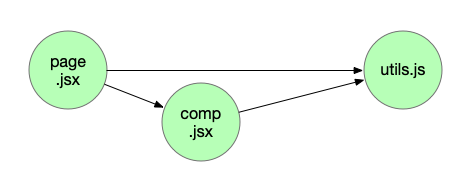
如果使用树的方式来维护，那么 utils.js 节点就会分别出现在 page.jsx 和 comp.jsx 的 children 中，出现冗余数据，在实际项目中这种情况会非常多。

但如果仅仅是体积的问题，可能还没那么严重，顶多费点空间成本。但我们又会发现，文件依赖还会出现这种循环依赖情况：

写 TypeScript 时在进行类型声明的时候，就经常会有这样循环依赖的情况。甚至两个文件之间也会循环依赖。这是合理的写法。

但是，这种写法对于直接使用链式树结构来说，如果创建链式树的算法是「在创建节点时，先创建子节点，待子节点创建返回后再完成自身的创建」的话，就不可能实现了，因为我们会发现，假如这样写就会出现无限依赖：

const fooTs = new Node({
  name: 'foo.ts',
  children: [
    new Node({
      name: 'bar.ts',
      children: [
        new Node({
          name: 'baz.ts',
          children: [
            new Node({
              name: 'foo.ts', // 和最顶的 foo.ts 是同一个
              children: [...] // 无限循环……
            })
          ]
        })
      ]
    })
  ]
})

此问题的根本原因是，这个关系是图的关系，而不是树的关系，所以在创建这个数据结构时，不能使用「在创建节点时，先创建子节点，待子节点创建返回后再完成自身的创建」算法，必须把思路切换回图的思路——先创建节点，再创建关系。

采用这种做法后，就相当于使用的是图的邻接链表结构了。我们来看看换成「先创建节点，再创建关系」后的写法：

// 先创建各节点，并且将 children 置为空数组
const fooTs = new Node({
  name: 'foo.ts',
  children: []
});

const barTs = new Node({
  name: 'bar.ts',
  children: []
});

const bazTs = new Node({
  name: 'baz.ts',
  children: []
});

// 然后再创建关系
fooTs.children.push(barTs);
barTs.children.push(bazTs);
bazTs.children.push(fooTs);

使用这种写法，就可以完成图的创建了。

但是，这种数据结构只能存在于内存当中，无法进行序列化，因为它是循环引用的。而无法进行序列化就意味着无法进行储存或传输，只能在自己进程里玩这样子，这显然是不行的。

所以还需要对数据结构进行改造，将邻接链表中的引用换成子指针表，也就是为每个节点添加一个索引，在 children 里使用索引来进行对应：

const graph = {
  nodes: [
    { id: 0, name: 'foo.ts', children: [1] },
    { id: 1, name: 'bar.ts', children: [2] },
    { id: 2, name: 'baz.ts', children: [0] }
  ]
}

这里会有同学问：为什么我们不直接用 nodes 的下标，而要再添加一个跟下标数字一样的 id 字段？原因很简单，因为下标是依赖数组本身的顺序的，如果一旦打乱了这个顺序——比如使用 filter 过滤出一部分节点出来，那这些下标就会发生变化。而添加一个 id 字段看起来有点冗余，但却为后面的算法降低了很多复杂度，更加具备可扩展性。

用栈来解决循环引用（有环有向图）的问题

当我们需要使用上面生成的这个依赖关系数据时，如果需要进行 DFS（深度遍历）或 BFS（广度遍历）算法进行遍历，就会发现由于这个依赖关系是循环依赖的，所以这些递归遍历算法是会死循环的。要解决这个问题很简单，有三个办法：

• 在已有图上添加一个字段来进行标记

每次进入遍历一个新节点时，先检查之前是否遍历过。但这种做法会污染这个图。

• 创建一个新的同样依赖关系的图，在这个新图中进行标记

这种做法虽然能实现，但比较麻烦，也浪费空间。

• 使用栈来记录遍历路径

我们创建一个数组作为栈，用以下规则执行：

每遍历一个节点，就往栈里压入新节点的索引（push）；

每从一个节点中返回，则移除栈中的顶部索引（pop）；

每次进入新节点前，先检测这个索引值是否已经在栈中存在（使用 includes），若存在则回退。

这种方式适用于 DFS 算法。

三、总结

依赖关系是源代码的另一种表达方式，也是把控巨型项目质量极为有利的工具。我们可以利用依赖关系挖掘出无数的想象空间，比如无用文件查找、版本间变动测试范围精确化等场景。若结合 Android、iOS、C++ 等底层依赖关系，就可以计算出更多的分析结果。

目前，依赖关系扫描工程是迭代式进行的，我们采用敏捷开发模式，从一些简单、粗略的 Bundle 级依赖关系，逐渐精确化到文件级甚至标识符级，在落地的过程中根据不同的精确度来逐渐满足对精度要求不同的需求，使得整个过程都可获得不同程度的收益和反馈，驱使我们不断持续迭代和优化。