N皇后问题的python实现
数据结构中常见的问题,最近复习到了,用python做一遍。
# 检测(x,y)这个位置是否合法(不会被其他皇后攻击到)
def is_attack(queue, x, y):
for i in range(x):
if queue[i] == y or abs(x - i) == abs(queue[i] - y):
return True
return False
# 按列来摆放皇后
def put_position(n, queue, col):
for i in range(n):
if not is_attack(queue, col, i):
queue[col] = i
if col == n - 1: # 此时最后一个皇后摆放好了,打印结果。
print(queue)
else:
put_position(n, queue, col + 1)
n = 4 # 这里是n 就是n皇后
queue = [None for i in range(n)] # 存储皇后位置的一维数组,数组下标表示皇后所在的列,下标对应的值为皇后所在的行。
put_position(n, queue, 0)
n = 4时:
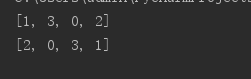
n = 8时:
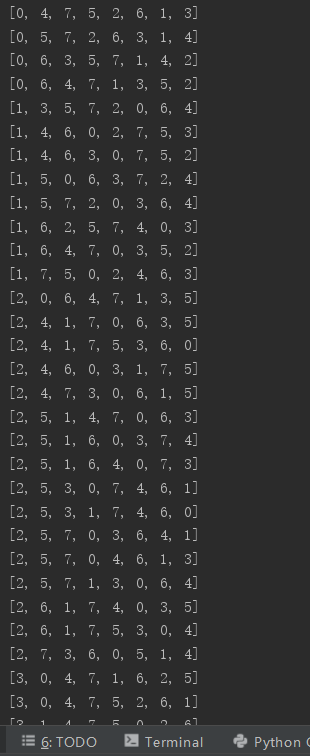
N皇后问题的python实现的更多相关文章
- 八皇后问题的Python实现和C#实现
看到八皇后问题的解决思路, 感觉很喜欢. 我用C#实现的版本之前贴在了百度百科上(https://baike.baidu.com/item/%E5%85%AB%E7%9A%87%E5%90%8E%E9 ...
- 8皇后问题(c++/python实现)
问题描述:在8*8的国际象棋盘上摆放8个皇后,使其不能互相攻击,即任何两个皇后都不能处于同一行.同一列或者同一斜线上,问有多少种摆法. 算法分析: 利用3个数组分表来标记冲突,数组a.b.c. a数组 ...
- 面试基础知识集合(python、计算机网络、操作系统、数据结构、数据库等杂记)
python python _.__.__xx__之间的差别 python中range.xrange和randrange的区别 python中 =.copy.deepcopy的差别 python 继承 ...
- Python学习二(生成器和八皇后算法)
看书看到迭代器和生成器了,一般的使用是没什么问题的,不过很多时候并不能用的很习惯 书中例举了经典的八皇后问题,作为一个程序员怎么能够放过做题的机会呢,于是乎先自己来一遍,于是有了下面这个ugly的代码 ...
- Python解决八皇后问题
最近看Python看得都不用tab键了,哈哈.今天看了一个经典问题--八皇后问题,说实话,以前学C.C++的时候有这个问题,但是当时不爱学,没搞会,后来算法课上又碰到,只是学会了思想,应该是学回溯法的 ...
- 八皇后,回溯与递归(Python实现)
八皇后问题是十九世纪著名的数学家高斯1850年提出 .以下为python语句的八皇后代码,摘自<Python基础教程>,代码相对于其他语言,来得短小且一次性可以打印出92种结果.同时可以扩 ...
- 【算法导论】八皇后问题的算法实现(C、MATLAB、Python版)
八皇后问题是一道经典的回溯问题.问题描述如下:皇后可以在横.竖.斜线上不限步数地吃掉其他棋子.如何将8个皇后放在棋盘上(有8*8个方格),使它们谁也不能被吃掉? 看到这个问题,最容易想 ...
- Python 八皇后问题
八皇后问题描述:在一个8✖️8的棋盘上,任意摆放8个棋子,要求任意两个棋子不能在同一行,同一列,同一斜线上,问有多少种解法. 规则分析: 任意两个棋子不能在同一行比较好办,设置一个队列,队列里的每个元 ...
- 【算法】八皇后问题 Python实现
[八皇后问题] 问题: 国际象棋棋盘是8 * 8的方格,每个方格里放一个棋子.皇后这种棋子可以攻击同一行或者同一列或者斜线(左上左下右上右下四个方向)上的棋子.在一个棋盘上如果要放八个皇后,使得她们互 ...
随机推荐
- javaScript 迭代器
for ...of 语句 "use strict"; var name = ['a','b','c']; var mark = [1, 2, 3]; for(var i of na ...
- Spring整合MyBatis整合
1.导入所需要的jar依赖 !--MyBatis和Spring的整合包 由MyBatis提供--> <dependency> <groupId>org.mybatis&l ...
- GEE windows 环境配置
参照GEE开发大神的一篇文章GEE学习笔记 三十五:windows下配置本地开发环境 - 无形的风的文章 - 知乎. 按他的顺序下来还是出了点问题,再整理一下自己遇到的问题. 1.安装Google的 ...
- xsxsxs
def getdecrype(l): a= length="" ): if(l[a]=="x"): break else: length+=l[a] a+= h ...
- 你真的懂git 吗
Git 存储目录结构介绍 首先我们先从 Git 存储目录说起,通过 git init 创建一个空的 Git 仓库,具体操作如下图: 创建完成后进入 .git 目录,如下图所示: hooks 该目录用于 ...
- 一口气讲完 LSA — PlSA —LDA在自然语言处理中的使用
自然语言处理之LSA LSA(Latent Semantic Analysis), 潜在语义分析.试图利用文档中隐藏的潜在的概念来进行文档分析与检索,能够达到比直接的关键词匹配获得更好的效果. LSA ...
- adb: failed to install app-debug.apk: Failure [INSTALL_FAILED_ABORTED: User rejected permissions]
一.使用adb 的usb真机调试,安装错误: adb: failed to install app-debug.apk: Failure [INSTALL_FAILED_ABORTED: User r ...
- Evolutionary approaches towards AI: past, present, and future
Evolutionary approaches towards AI: past, present, and future 2019-10-06 07:28:13 This blog is from: ...
- XML External Entity Injection(XXE)
写在前面 安全测试fortify扫描接口项目代码,暴露出标题XXE的问题, 记录一下.官网链接: https://www.owasp.org/index.php/XML_External_Entity ...
- 脚本备份MySQL数据库和binlog日志
用Mysqldump实现全库备份+binlog的数据还原 首先是为mysql做指定库文件的全库备份 vim mysqlbak.sh #!/bin/bash #定义数据库目录,要能找到mysqldump ...
