概率（Probability）：事件发生的可能性的数值度量。

组合（Combination）：从n项中选取r项的组合数，不考虑排列顺序。组合计数法则：。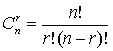

排列（Permutation）：从n项中选取r项的组合数，考虑排列顺序。排列计数法则：。

贝叶斯定理（Bayes's Theorem）：获取新信息后对概率进行修正的一种方法。先验概率--->新信息--->应用贝叶斯定理--->后验概率。具体请见：贝叶斯定理推导（Bayes's Theorem）。

离散型概率分布（Discrete Probability Distribution）：伯努利分布，二项分布，泊松分布，几何分布，超几何分布，多项分布

连续型概率分布（Continous Probability Distribution）：指数分布，正态分布，均匀分布

抽样概率分布（Sampling Probability Distribution）：t分布，卡方分布，F分布

常见的概率分布类型（一）（Probability Distribution I）

常见的概率分布类型（二）（Probability Distribution II）

概率质量函数 (Probability Mass Function，pmf)：离散随机变量在各特定取值上的概率。

概率密度函数（Probability Density Function，pdf）：连续随机变量在一定区间内取值的概率， 不直接给出概率值，曲线下的面积才是概率，需要通过对这段区间进行积分来求。

（注：曲线下单个点的面积为0，所以连续随机变量取某一特定值的概率是0。）

累积分布函数（Cumulative Distribution Function，CDF）：对于离散分布，cdf可以通过定义得到，而其函数形状应该是阶梯状的；对连续函数，是所有小于等于a的值出现概率的和，即F(a)=P(x<=a)，可以通过对概率密度函数积分得到。

概率论基础知识（Probability Theory）的更多相关文章

  1. PGM：概率论基础知识

    http://blog.csdn.net/pipisorry/article/details/52459847 概率图模型PGM:概率论基础知识 独立性与条件独立性 独立性 条件独立性 也就是表示给定 ...

  2. PRML 基础知识

    1 一个经典例子 ​ 一个经典的例子就是Polynomial Curve Fitting问题,现在将以此为基础介绍一些基本概念和方法.该问题的主要思路是针对给定的训练集\(\mathbf{x}\equ ...

  3. 一起啃PRML - 1.2 Probability Theory 概率论

    一起啃PRML - 1.2 Probability Theory @copyright 转载请注明出处 http://www.cnblogs.com/chxer/ A key concept in t ...

  4. 逻辑回归Logistic Regression 之基础知识准备

    0. 前言   这学期 Pattern Recognition 课程的 project 之一是手写数字识别,之二是做一个网站验证码的识别(鸭梨不小哇).面包要一口一口吃,先尝试把模式识别的经典问题—— ...

  5. .NET面试题系列[1] - .NET框架基础知识(1)

    很明显,CLS是CTS的一个子集,而且是最小的子集. - 张子阳 .NET框架基础知识(1) 参考资料: http://www.tracefact.net/CLR-and-Framework/DotN ...

  6. RabbitMQ基础知识

    RabbitMQ基础知识 一.背景 RabbitMQ是一个由erlang开发的AMQP(Advanced Message Queue )的开源实现.AMQP 的出现其实也是应了广大人民群众的需求,虽然 ...

  7. Java基础知识（壹）

    写在前面的话 这篇博客,是很早之前自己的学习Java基础知识的,所记录的内容,仅仅是当时学习的一个总结随笔.现在分享出来,希望能帮助大家,如有不足的,希望大家支出. 后续会继续分享基础知识手记.希望能 ...

  8. selenium自动化基础知识

    什么是自动化测试? 自动化测试分为:功能自动化和性能自动化 功能自动化即使用计算机通过编码的方式来替代手工测试,完成一些重复性比较高的测试,解放测试人员的测试压力.同时,如果系统有不份模块更改后,只要 ...

  9. [SQL] SQL 基础知识梳理（一）- 数据库与 SQL

    SQL 基础知识梳理(一)- 数据库与 SQL [博主]反骨仔 [原文地址]http://www.cnblogs.com/liqingwen/p/5902856.html 目录 What's 数据库 ...

随机推荐

  1. (算法)LeetCode刷题

    LeetCode 56 合并区别 Given [1,3],[2,6],[8,10],[15,18], return [1,6],[8,10],[15,18]. 关键就是a[1]>=b[0] 也就 ...

  2. ReentrantLock 锁释放源码分析

    ReentrantLock 锁释放源码分析: 调用的是unlock 的方法: public void unlock() { sync.release(1); } 接下来分析release() 方法: ...

  3. Docker 部署ELK之Sentinl日志报警

    前篇文章简单介绍了Docker 部署ELK,以及使用filebeat收集java日志.这篇我们介绍下日志报警配置,这里我们使用Sentinl插件. 1.修改kibana参数 进入elk容器,修改对应参 ...

  4. scala基础题--面向对象1

    练习1 编写computer类,包含CPU.内存.硬盘等属性,getDetails方法用于返回computer的详细信息. 编写PC子类,继承computer类,添加特有属性[品牌brand] 编写n ...

  5. 汇编语言01 - 打印 "Hello World!"

    Hello World! 源代码 data segment msg db "Hello World!$";定义名称为msg的字符串,最后加上$,表示字符串结束 data ends ...

  6. Redis（七）持久化(Persistence)

    前言 前文中介绍到Redis时内存的K-V数据结构存储服务器.Redis的高性能原因之一在于其读写数据都是在内存中进行.它的架构实现方式决定了Redis的数据存储具有不可靠性,易丢失,因为RAM内存在 ...

  7. sprintboot动态静态资源转发

    背景|     要做一个功能,根据规则服务器上创建文件后,返回可下载的链接           因为sprintboot中地址需要先在用@RequestMapping定义好,否则解析不了,这时动态生成 ...

  8. C语言语法教程-链表

    链表是一群结构体(称为结点)通过指针连起来.这种结构体类型,比较特殊,叫自引用结构体类型.它有一个指针指向和和结构体一样的类型,其余是数据成员. 头指针指向第一结点,尾指针一定要用空表示,这叫有头有尾 ...

  9. codeforces #577(Div.2)

    codeforces #577(Div.2) A  Important Exam A class of students wrote a multiple-choice test. There are ...

  10. Matlab空对象模式

    在空对象模式(Null Object Pattern)中,一个空对象取代 NULL 对象实例的检查.Null 对象不是检查空值,而是反应一个不做任何动作的关系.这样的 Null 对象也可以在数据不可用 ...