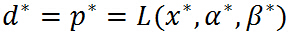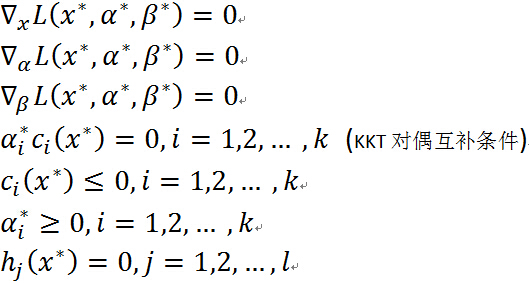简易解说拉格朗日对偶(Lagrange duality)(转载)
转载自https://www.cnblogs.com/90zeng/p/Lagrange_duality.html,本人觉得讲的非常好!
1.原始问题
假设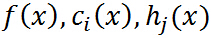 是定义在
是定义在 上的连续可微函数(为什么要求连续可微呢,后面再说,这里不用多想),考虑约束最优化问题:
上的连续可微函数(为什么要求连续可微呢,后面再说,这里不用多想),考虑约束最优化问题:
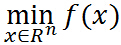
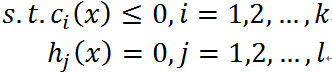
称为约束最优化问题的原始问题。
现在如果不考虑约束条件,原始问题就是:
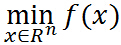
因为假设其连续可微,利用高中的知识,对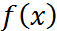 求导数,然后令导数为0,就可解出最优解,很easy. 那么,问题来了(呵呵。。。),偏偏有约束条件,好烦啊,要是能想办法把约束条件去掉就好了,bingo! 拉格朗日函数就是干这个的。
求导数,然后令导数为0,就可解出最优解,很easy. 那么,问题来了(呵呵。。。),偏偏有约束条件,好烦啊,要是能想办法把约束条件去掉就好了,bingo! 拉格朗日函数就是干这个的。
引进广义拉格朗日函数(generalized Lagrange function):
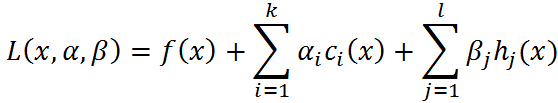
不要怕这个式子,也不要被拉格朗日这个高大上的名字给唬住了,让我们慢慢剖析!这里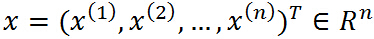 ,
, 是拉格朗日乘子(名字高大上,其实就是上面函数中的参数而已),特别要求
是拉格朗日乘子(名字高大上,其实就是上面函数中的参数而已),特别要求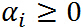 .
.
现在,如果把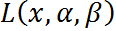 看作是关于
看作是关于 的函数,要求其最大值,即
的函数,要求其最大值,即
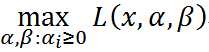
再次注意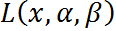 是一个关于
是一个关于 的函数,经过我们优化(不要管什么方法),就是确定
的函数,经过我们优化(不要管什么方法),就是确定 的值使得
的值使得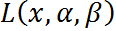 取得最大值(此过程中把
取得最大值(此过程中把 看做常量),确定了
看做常量),确定了 的值,就可以得到
的值,就可以得到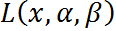 的最大值,因为
的最大值,因为 已经确定,显然最大值
已经确定,显然最大值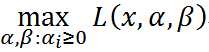 就是只和
就是只和 有关的函数,定义这个函数为:
有关的函数,定义这个函数为:
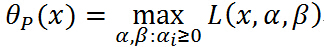
其中 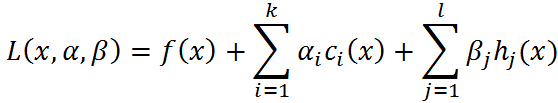
下面通过 是否满足约束条件两方面来分析这个函数:
是否满足约束条件两方面来分析这个函数:
- 考虑某个
 违反了原始的约束,即
违反了原始的约束,即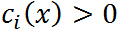 或者
或者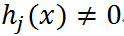 ,那么:
,那么:
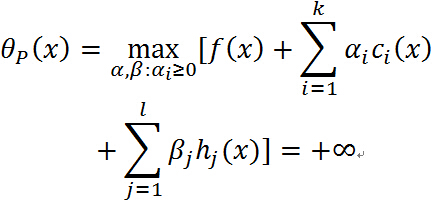
注意中间的最大化式子就是确定 的之后的结果,若
的之后的结果,若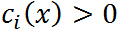 ,则令
,则令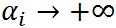 ,如果
,如果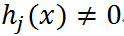 ,很容易取值
,很容易取值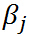 使得
使得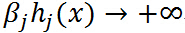
- 考虑
 满足原始的约束,则:
满足原始的约束,则: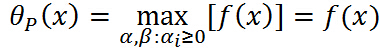 ,注意中间的最大化是确定
,注意中间的最大化是确定 的过程,
的过程,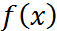 就是个常量,常量的最大值显然是本身.
就是个常量,常量的最大值显然是本身.
通过上面两条分析可以得出:

那么在满足约束条件下:
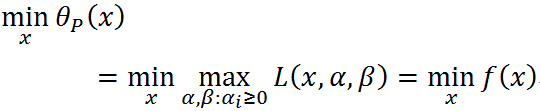
即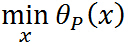 与原始优化问题等价,所以常用
与原始优化问题等价,所以常用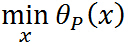 代表原始问题,下标 P 表示原始问题,定义原始问题的最优值:
代表原始问题,下标 P 表示原始问题,定义原始问题的最优值:
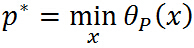
原始问题讨论就到这里,做一个总结:通过拉格朗日这位大神的办法重新定义一个无约束问题(大家都喜欢无拘无束),这个无约束问题等价于原来的约束优化问题,从而将约束问题无约束化!
2.对偶问题
定义关于 的函数:
的函数:
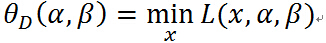
注意等式右边是关于 的函数的最小化,
的函数的最小化, 确定以后,最小值就只与
确定以后,最小值就只与 有关,所以是一个关于
有关,所以是一个关于 的函数.
的函数.
考虑极大化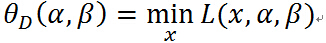 ,即
,即
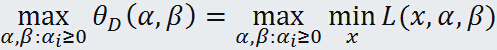
这就是原始问题的对偶问题,再把原始问题写出来:
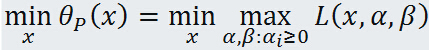
形式上可以看出很对称,只不过原始问题是先固定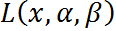 中的
中的 ,优化出参数
,优化出参数 ,再优化最优
,再优化最优 ,而对偶问题是先固定
,而对偶问题是先固定 ,优化出最优
,优化出最优 ,然后再确定参数
,然后再确定参数 .
.
定义对偶问题的最优值:
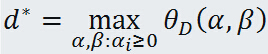
3. 原始问题与对偶问题的关系
定理:若原始问题与对偶问题都有最优值,则
证明:对任意的 和
和 ,有
,有
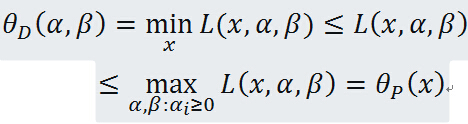
即

由于原始问题与对偶问题都有最优值,所以
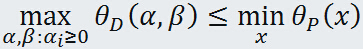
即
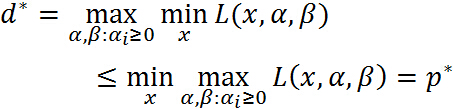
也就是说原始问题的最优值不小于对偶问题的最优值,但是我们要通过对偶问题来求解原始问题,就必须使得原始问题的最优值与对偶问题的最优值相等,于是可以得出下面的推论:
推论:设
分别是原始问题和对偶问题的可行解,如果
,那么
分别是原始问题和对偶问题的最优解。
所以,当原始问题和对偶问题的最优值相等: 时,可以用求解对偶问题来求解原始问题(当然是对偶问题求解比直接求解原始问题简单的情况下),但是到底满足什么样的条件才能使的
时,可以用求解对偶问题来求解原始问题(当然是对偶问题求解比直接求解原始问题简单的情况下),但是到底满足什么样的条件才能使的 呢,这就是下面要阐述的 KKT 条件
呢,这就是下面要阐述的 KKT 条件
4. KKT 条件
定理:对于原始问题和对偶问题,假设函数
和
是凸函数,
是仿射函数(即由一阶多项式构成的函数,f(x)=Ax + b, A是矩阵,x,b是向量);并且假设不等式约束
是严格可行的,即存在
,对所有
有
,则存在
,使得
是原始问题的最优解,
是对偶问题的最优解,并且
定理:对于原始问题和对偶问题,假设函数
和
是凸函数,
是仿射函数(即由一阶多项式构成的函数,f(x)=Ax + b, A是矩阵,x,b是向量);并且假设不等式约束
是严格可行的,即存在
,对所有
有
,则
分别是原始问题和对偶问题的最优解的充分必要条件是
满足下面的Karush-Kuhn-Tucker(KKT)条件:
关于KKT 条件的理解:前面三个条件是由解析函数的知识,对于各个变量的偏导数为0(这就解释了一开始为什么假设三个函数连续可微,如果不连续可微的话,这里的偏导数存不存在就不能保证),后面四个条件就是原始问题的约束条件以及拉格朗日乘子需要满足的约束。
特别注意当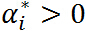 时,由KKT对偶互补条件可知:
时,由KKT对偶互补条件可知: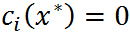 ,这个知识点会在 SVM 的推导中用到.
,这个知识点会在 SVM 的推导中用到.
5. 总结
一句话,某些条件下,把原始的约束问题通过拉格朗日函数转化为无约束问题,如果原始问题求解棘手,在满足KKT的条件下用求解对偶问题来代替求解原始问题,使得问题求解更加容易。
简易解说拉格朗日对偶(Lagrange duality)(转载)的更多相关文章
- 简易解说拉格朗日对偶(Lagrange duality)(转载)
引言:尝试用最简单易懂的描述解释清楚机器学习中会用到的拉格朗日对偶性知识,非科班出身,如有数学专业博友,望多提意见! 1.原始问题 假设是定义在上的连续可微函数(为什么要求连续可微呢,后面再说,这里不 ...
- 简易解说拉格朗日对偶(Lagrange duality)
引言:尝试用最简单易懂的描述解释清楚机器学习中会用到的拉格朗日对偶性知识,非科班出身,如有数学专业博友,望多提意见! 1.原始问题 假设是定义在上的连续可微函数(为什么要求连续可微呢,后面再说,这里不 ...
- 拉格朗日对偶性(Lagrange duality)
目录 拉格朗日对偶性(Lagrange duality) 1. 从原始问题到对偶问题 2. 弱对偶与强对偶 3. KKT条件 Reference: 拉格朗日对偶性(Lagrange duality) ...
- SVM小白教程(2):拉格朗日对偶
在上一篇文章中,我们推导出了 SVM 的目标函数: \[ \underset{(\mathbf{w},b)}{\operatorname{min}} ||\mathbf{w}|| \\ \operat ...
- Support Vector Machine(2):Lagrange Duality求解线性可分SVM的最佳边界
在上篇文章<Support Vector Machine(1):线性可分集的决策边界>中,我们最后得到,求SVM最佳Margin的问题,转化为了如下形式: 到这一步后,我个人又花了很长的时 ...
- 拉格朗日对偶(Lagrange duality)
拉格朗日对偶(Lagrange duality) 存在等式约束的极值问题求法,比如下面的最优化问题: 目标函数是f(w),下面是等式约束.通常解法是引入拉格朗日算子,这里使用 ...
- SVM(支持向量机)(二)—Lagrange Duality(拉格朗日对偶问题)
(整理自AndrewNG的课件,转载请注明.整理者:华科小涛@http://www.cnblogs.com/hust-ghtao/) SVM有点让人头疼,但还是要弄明白.把这一大块搞懂了,会很有成就感 ...
- 拉格朗日(Lagrange)插值算法
拉格朗日插值(Lagrange interpolation)是一种多项式插值方法,指插值条件中不出现被插函数导数值,过n+1个样点,满足如下图的插值条件的多项式.也叫做拉格朗日公式. 这里以拉格朗日 ...
- 3. SVM分类器求解(1)——Lagrange duality
先抛开上面的二次规划问题,先来看看存在等式约束的极值问题求法,比如下面的最优化问题: 目标函数是f(w),下面是等式约束.通常解法是引入拉格朗日算子,这里使用来表示算子,得到拉格朗日公式为 是等式约束 ...
随机推荐
- web-文件包含
提示 构造payload ?file=flag.php 得到一串字符,那么我们用PHP伪协议尝试一下 构造payload ?file=php://filter/read=convert.base64- ...
- 《Zabbix》
https://github.com/itnihao/zabbix-rpm https://github.com/itnihao/zabbix-book 一.zabbix支持的主要监控方式: zabb ...
- SCOI 2005 互不侵犯
洛谷 P1896 [SCOI2005]互不侵犯 洛谷传送门 题目描述 在N×N的棋盘里面放K个国王,使他们互不攻击,共有多少种摆放方案.国王能攻击到它上下左右,以及左上左下右上右下八个方向上附近的各一 ...
- python-文件操作&模块&面向对象
python 文件处理 li = [[']] for i in li: print(','.join(i)) # join字符串拼接 语文,数学,英语 100,122,123 从原文件末尾开始写入 # ...
- mysql group by 的用法解析
1. group by的常规用法 group by的常规用法是配合聚合函数,利用分组信息进行统计,常见的是配合max等聚合函数筛选数据后分析,以及配合having进行筛选后过滤. 聚合函数max se ...
- hdu6492 暴力预处理 + 枚举
http://acm.hdu.edu.cn/showproblem.php?pid=6492 题意 他们一共有 n+m+2k 个人,包括 n+k 个男生,m+k 个女生,其中 k 对男女生为异性情侣, ...
- 对mglearn库的理解(转)
https://blog.csdn.net/az9996/article/details/86490496
- 数据仓库002 - 复习Linux shell命令 - echo bash_profile bashrc which命令的理解 alias history
1.echo 打印 . echo 的作用是在屏幕上打印输出内容,与文件和持久化可以理解为没有丝毫关联.如:在屏幕上打印“ echo 的作用是打印文字! ” 实例1:输出系统的环境变量名称 $PATH ...
- Java网络传输数据加密算法
算法可逆,具有跨平台特性 import java.io.IOException; import java.io.UnsupportedEncodingException; import java.se ...
- Oracle数据库rownum用法集锦
Oracle中rownum可以用来限制查询 具体用法: 1.返回查询集合中的第1行 select * from tableName where rownum = 1 2.返回查询集合中的第2行 错误示 ...