c# 画正态分布图

  /// <summary>
    /// 提供正态分布的数据和图片
    /// </summary>
    public class StandardDistribution
    {

        /// <summary>
        /// 样本数据
        /// </summary>
        public List<double> Xs { get; private set; }

        public StandardDistribution(List<double> Xs)
        {
            this.Xs = Xs;

            Average = Xs.Average();
            Variance = GetVariance(Xs);

            if (Variance == 0) throw new Exception("方差为0");//此时不需要统计 因为每个样本数据都相同，可以在界面做相应提示

            StandardVariance = Math.Sqrt(Variance);
        }

        /// <summary>
        /// 方差/标准方差的平方
        /// </summary>
        public double Variance { get; private set; }

        /// <summary>
        /// 标准方差
        /// </summary>
        public double StandardVariance { get; private set; }

        /// <summary>
        /// 算数平均值/数学期望
        /// </summary>
        public double Average { get; private set; }

        /// <summary>
        /// 1/ (2π的平方根)的值
        /// </summary>
        public static double InverseSqrt2PI = 1 / Math.Sqrt(2 * Math.PI);

        /// <summary>
        /// 获取指定X值的Y值  计算正太分布的公式
        /// </summary>
        /// <param name="x"></param>
        /// <returns></returns>
        public double GetGaussianDistributionY(double x)
        {
            double PowOfE = -(Math.Pow(Math.Abs(x - Average), 2) / (2 * Variance));

            double result = (StandardDistribution.InverseSqrt2PI / StandardVariance) * Math.Pow(Math.E, PowOfE);

            return result;
        }

        /// <summary>
        /// 获取正太分布的坐标<x,y>
        /// </summary>
        /// <returns></returns>
        public List<Tuple<double, double>> GetGaussianDistributionYs()
        {
            List<Tuple<double, double>> XYs = new List<Tuple<double, double>>();

            Tuple<double, double> xy = null;

            foreach (double x in Xs)
            {
                xy = new Tuple<double, double>(x, GetGaussianDistributionY(x));
                XYs.Add(xy);
            }

            return XYs;
        }

        /// <summary>
        /// 获取整型列表的方差
        /// </summary>
        /// <param name="src">要计算方差的数据列表</param>
        /// <returns></returns>
        public static double GetVariance(List<double> src)
        {
            double average = src.Average();
            double SumOfSquares = 0;
            src.ForEach(x => { SumOfSquares += Math.Pow(x - average, 2); });
            return SumOfSquares / src.Count;//方差
        }

        /// <summary>
        /// 获取整型列表的方差
        /// </summary>
        /// <param name="src">要计算方差的数据列表</param>
        /// <returns></returns>
        public static float GetVariance(List<float> src)
        {
            float average = src.Average();
            double SumOfSquares = 0;
            src.ForEach(x => { SumOfSquares += Math.Pow(x - average, 2); });
            return (float)SumOfSquares / src.Count;//方差
        }

        /// <summary>
        /// 画学生成绩的正态分布
        /// </summary>
        /// <param name="Width"></param>
        /// <param name="Height"></param>
        /// <param name="Scores">分数，Y值</param>
        /// <param name="familyName"></param>
        /// <returns></returns>
        public  Bitmap GetGaussianDistributionGraph(int Width, int Height,int TotalScore, string familyName = "宋体")
        {
            //横轴 分数；纵轴 正态分布的值

            Bitmap bitmap = new Bitmap(Width, Height);

            Graphics gdi = Graphics.FromImage(bitmap);

            gdi.Clear(Color.White);
            gdi.SmoothingMode = SmoothingMode.HighQuality;
            gdi.TextRenderingHint = TextRenderingHint.ClearTypeGridFit;
            gdi.PixelOffsetMode = PixelOffsetMode.HighQuality;

            List<Tuple<double, double>> Scores = GetGaussianDistributionYs().OrderBy(x => x.Item1).ToList();//排序 方便后面点与点之间的连线  保证 分数低的 在左边

            float YHeight = 0.8F * Height;// 相对左下角 YHeight*0.9F 将表示 maxY
            float XWidth = 0.9F * Width;//相对左下角 XWidth*0.9F 将表示 maxX

            float marginX = (Width - XWidth) / 2F;//x轴相对左右图片边缘的像素
            float marginY = (Height - YHeight) / 2F;//y轴相对上下图片边缘的像素

            PointF leftTop = new PointF(marginX, marginY);

            PointF leftBottom = new PointF(marginX, marginY + YHeight);//坐标轴的左下角

            PointF rightBottom = new PointF(marginX + XWidth, marginY + YHeight);//坐标轴的右下角

            gdi.DrawLine(Pens.Gray, leftBottom, rightBottom);//x轴
            gdi.DrawLine(Pens.Gray, leftBottom, leftTop);//Y轴

            //两个箭头 四条线 6个坐标 另需4个坐标

            PointF YArrowLeft = new PointF(leftTop.X - 5, leftTop.Y + 5);
            PointF YArrowRight = new PointF(leftTop.X + 5, leftTop.Y + 5);
            PointF XArrowTop = new PointF(rightBottom.X - 5, rightBottom.Y - 5);
            PointF XArrowBottom = new PointF(rightBottom.X - 5, rightBottom.Y + 5);

            gdi.DrawLine(Pens.Gray, leftTop, YArrowLeft);
            gdi.DrawLine(Pens.Gray, leftTop, YArrowRight);
            gdi.DrawLine(Pens.Gray, rightBottom, XArrowTop);
            gdi.DrawLine(Pens.Gray, rightBottom, XArrowBottom);

            float unitX = 0.0F;//X轴转换比率
            float unitY = 0.0F;//Y轴转换比率

            List<PointF> pointFs = ConvertToPointF(Scores, XWidth * 0.9F, YHeight * 0.9F, leftTop, out unitX, out unitY);//将分数和概率 转换成 坐标

            gdi.DrawCurve(Pens.Black, pointFs.ToArray(), 0.0F);//基数样条

            //平均分 与 Y轴平行

            PointF avg_top = new PointF(leftTop.X + (float)Average * unitX, leftTop.Y);
            PointF avg_bottom = new PointF(leftTop.X + (float)Average * unitX, leftBottom.Y);
            gdi.DrawLine(Pens.Black, avg_top, avg_bottom);
            gdi.DrawString(string.Format("{0}", ((float)Average ).ToString("F2")), new Font("宋体", 11), Brushes.Black, avg_bottom.X, avg_bottom.Y-25);

            //将期望和方差写在横轴下方中间

            PointF variance_pf = new PointF(leftBottom.X+(XWidth/2)-120, avg_bottom.Y + 25);
            gdi.DrawString(string.Format("期望：{0}；方差：{1}", ((float)Average).ToString("F2"), Variance.ToString("F2")), new Font("宋体", 11), Brushes.Black, variance_pf.X, variance_pf.Y);

            //将最小分数 和 最大分数 分成9段 标记在坐标轴横轴上

            double minX = Scores.Min(x => x.Item1);
            double maxX = Scores.Max(x => x.Item1);

            double perSegment = TotalScore/10;// (maxX - minX) / 9F;//每一段表示的分数

            List<double> segs = new List<double>();//每一个分段分界线横轴的值

            segs.Add(leftBottom.X + (float)minX * unitX);

            for (int i = 1; i < 11; i++)
            {
                segs.Add(leftBottom.X + (float)minX * unitX + perSegment * i * unitX);
            }
            for (int i = 0; i < 11; i++)
            {
                gdi.DrawPie(Pens.Black, (float)segs[i] - 1, leftBottom.Y - 1, 2, 2, 0, 360);

                gdi.DrawString(string.Format("{0}", ((minX + perSegment * (i))).ToString("F0")), new Font("宋体", 11), Brushes.Black, (float)segs[i] - 15, leftBottom.Y + 5);
            }

            return bitmap;
        }

        /// <summary>
        /// 将数据转换为坐标
        /// </summary>
        /// <param name="Scores"></param>
        /// <param name="X">最长利用横轴</param>
        /// <param name="Y">最长利用纵轴 </param>
        /// <param name="leftTop">左上角原点</param>
        /// <returns></returns>
        private static List<PointF> ConvertToPointF(List<Tuple<double, double>> Scores, float X, float Y, PointF leftTop, out  float unitX, out  float unitY)
        {
            double maxY = Scores.Max(x => x.Item2);
            double maxX = Scores.Max(x => x.Item1);

            List<PointF> result = new List<PointF>();

            float paddingY = Y * 0.01F;
            float paddingX = X * 0.01F;

            unitY = (float)((Y - paddingY) / maxY);//单位纵轴表示出来需要的高度 计算出来的纵坐标需要 leftTop.Y+(Y-item2*unitY)+paddingY
            unitX = (float)((X - paddingX) / maxX);//单位横轴表示出来需要的宽度 计算出来的横坐标需要 leftTop.X+item1*unitX

            PointF pf = new PointF();
            foreach (Tuple<double, double> item in Scores)
            {
                pf = new PointF(leftTop.X + (float)item.Item1 * unitX, leftTop.Y + (Y - (float)item.Item2 * unitY) + paddingY);
                result.Add(pf);
            }

            return result;
        }

    }

调用：

            StandardDistribution mathX = new StandardDistribution(scores);
            Bitmap bitmap = mathX.GetGaussianDistributionGraph(800, 480, totalScore);
            bitmap.Save("tt.jpg", System.Drawing.Imaging.ImageFormat.Jpeg);

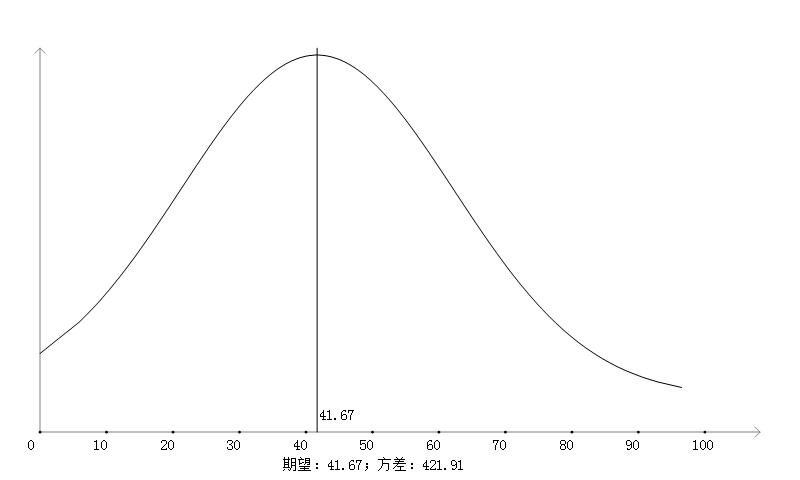
测试数据生成的正态分布图：