雅礼集训 2017 Day4 编码（2-sat）

题意

题目链接：https://loj.ac/problem/6036

思路

​ 首先，有前缀关系的串不能同时存在，不难看出这是一个 2-sat 问题。先假设所有串都带问号，那么每一个字符串，我们可以把它的两种情况当成一个布尔值的 \(0/1\) 。然后互为前缀的串不能同时存在，最多连 \(n^2\) 条边，直接跑 2-sat 就在 \({\cal O}(n^2)\) 的时间内解决了本题。

​ 由于是个 \(01\) 字符串的前缀问题，我们不难想到字典树。要是能在字典树上体现前缀关系就好了。我们先退而求其次，先表达链式结构。

​ 我个人习惯用一个被划成两半的点来表示一个布尔值，左部分表示假，右部分表示真。就像这样：

​ 我们现在的问题是，对于 \(n\) 个布尔值，如何通过 \(\mathcal O(n)\) 建图表示这些布尔值最多只能存在一个真。化成 2-sat 的语言：它们两两的与运算都为 \(0\) 。

​ 这就是 2-sat 的前缀优化。再开一排新布尔值（用方形点来表示），采用下图方式连边：

​ 千言万语都不如一张图讲的清楚。你会发现，不管哪个原布尔值取了 \(1\) ，都可以通过方点告诉其他节点，“这条链里已经有人是真了，你们其他人都不能是真。”

​ 要特别注意的一点是，逆否边都是要连的，上图只是为了方便没有画出逆否边，具体写代码的时候也可以在连边函数中加上连逆否边防止忘连。

​ 有机化学都白学了吗？快告诉我上面的链中的链节是什么？

​ 不管有多长的链，都可以通过这种基团相连，处在同一链上的布尔值最多只有一个真。

​ 那么，树上的做法也就很显然了。

​ 上图就是一种树上的结构（例子举的不大好，请读者自行脑补一些树枝），它在字典树上看是这样的：

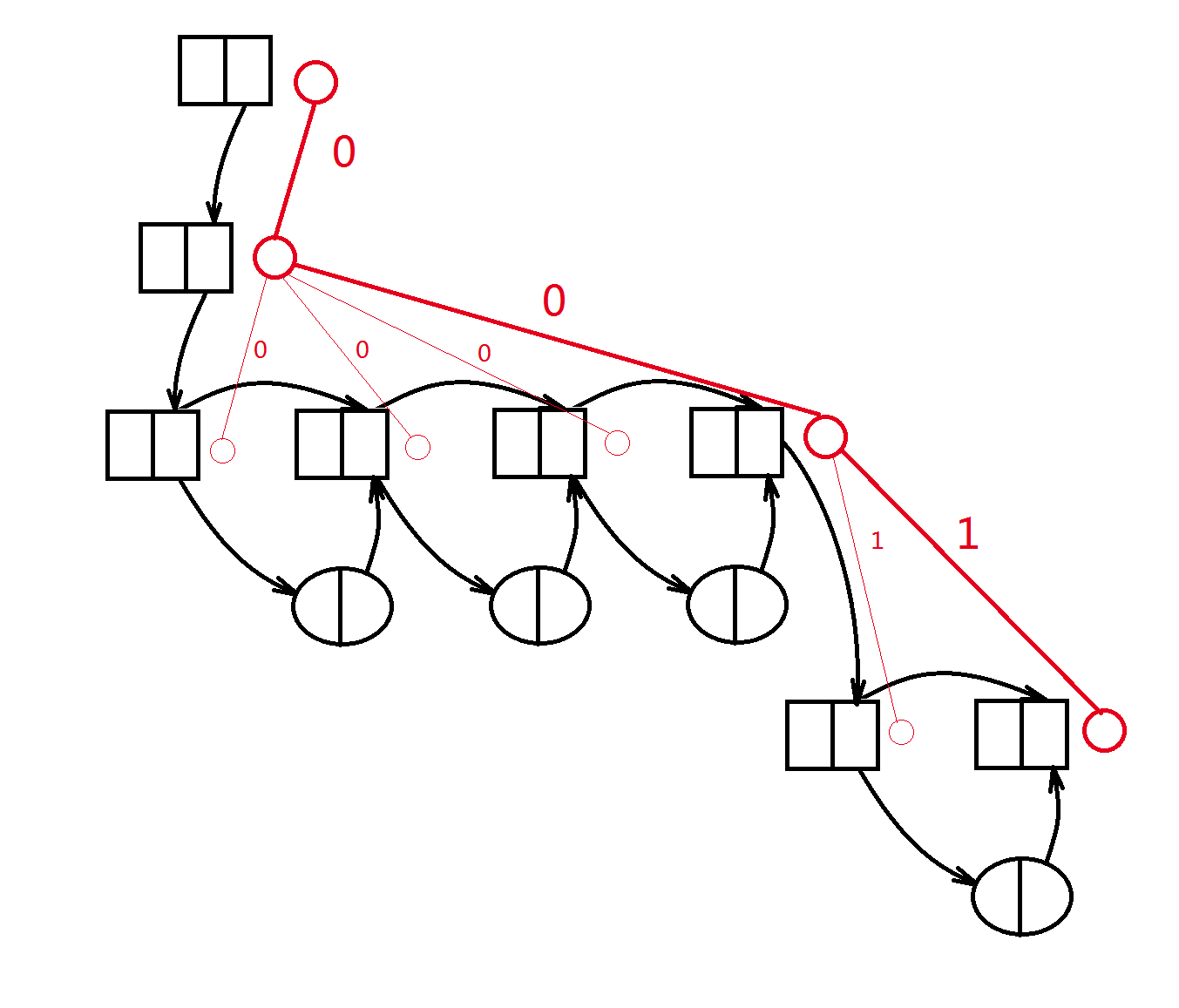
​ 上图的字典树中插入了 \(00,00,00,001\) 四个串，树上的一条向上的路径中不会同时有多个为真的布尔值。好写起见，我们索性在插入完一个串后的在字典树上可持久化出一个位置，插入我们的基团。这样写的话插入字符串要按长度升序来插。

代码

#include<bits/stdc++.h>
#define FOR(i, x, y) for(int i = (x), i##END = (y); i <= i##END; ++i)
#define DOR(i, x, y) for(int i = (x), i##END = (y); i >= i##END; --i)
template<typename T, typename _T> inline bool chk_min(T &x, const _T &y) {return y < x ? x = y, 1 : 0;}
template<typename T, typename _T> inline bool chk_max(T &x, const _T &y) {return x < y ? x = y, 1 : 0;}
typedef long long ll;
const int N = 500005 * 6;
const int M = 500005 * 16;

template<const int N, const int M, typename T> struct Linked_List
{
	int head[N], nxt[M], tot; T to[M];
	Linked_List() {clear();}
	T &operator [](const int x) {return to[x];}
	void clear() {memset(head, -1, sizeof(head)), tot = 0;}
	void add(int u, T v) {to[tot] = v, nxt[tot] = head[u], head[u] = tot++;}
	#define EOR(i, G, u) for(int i = G.head[u]; ~i; i = G.nxt[i])
};

Linked_List<N, M, int> G;

int rt, tot, ch[N][2];
int dfn[N], low[N], stk[N], bel[N], dfn_idx, scc, tp;
std::string str[N]; int ord[N];
int n, m;

bool cmp(int a, int b) {return str[a].length() < str[b].length();}

void tarjan(int u, int fa_e)
{
	dfn[u] = low[u] = ++dfn_idx, stk[++tp] = u;
	EOR(i, G, u)
	{
		if(i == (fa_e ^ 1)) continue;
		int v = G[i];
		if(!dfn[v])
		{
			tarjan(v, i);
			chk_min(low[u], low[v]);
		}
		else if(!bel[v] && dfn[v] < dfn[u])
			chk_min(low[u], dfn[v]);
	}
	if(dfn[u] == low[u])
	{
		scc++;
		do bel[stk[tp]] = scc; while(stk[tp--] != u);
	}
}

void link(int u, int v)
{
	G.add(u, v), G.add(v ^ 1, u ^ 1);
}

void insert(std::string &str, int t)
{
	if(!rt) rt = ++tot;
	int k = rt, las;
	FOR(i, 0, (int)str.length() - 1)
	{
		if(!ch[k][str[i] - '0'])
		{
			ch[k][str[i] - '0'] = ++tot;
			link(k << 1 | 1, ch[k][str[i] - '0'] << 1 | 1);
		}
		las = k, k = ch[k][str[i] - '0'];
	}
	tot++;
	link(k << 1 | 1, tot << 1 | 1);
	link(t, tot << 1 | 1);
	link(k << 1 | 1, t ^ 1);
	ch[las][str[(int)str.length() - 1] - '0'] = tot;
}

int main()
{
	scanf("%d", &n);
	rt = 0, tot = n;
	FOR(i, 1, n) std::cin >> str[i], ord[i] = i;
	std::sort(ord + 1, ord + 1 + n, cmp);
	FOR(i, 1, n)
	{
		bool flg = 0;
		FOR(j, 0, (int)str[ord[i]].length() - 1) if(str[ord[i]][j] == '?')
		{
			str[ord[i]][j] = '0', insert(str[ord[i]], i << 1);
			str[ord[i]][j] = '1', insert(str[ord[i]], i << 1 | 1);
			flg = 1;
			break;
		}
		if(!flg)
		{
			insert(str[ord[i]], i << 1);
			link(i << 1 | 1, i << 1);
		}
	}
	FOR(i, 2, tot << 1 | 1) if(!dfn[i]) tarjan(i, -1);
	FOR(i, 1, tot) if(bel[i << 1] == bel[i << 1 | 1])
	{
		puts("NO");
		return 0;
	}
	puts("YES");
	return 0;
}