noip模拟赛 入阵曲

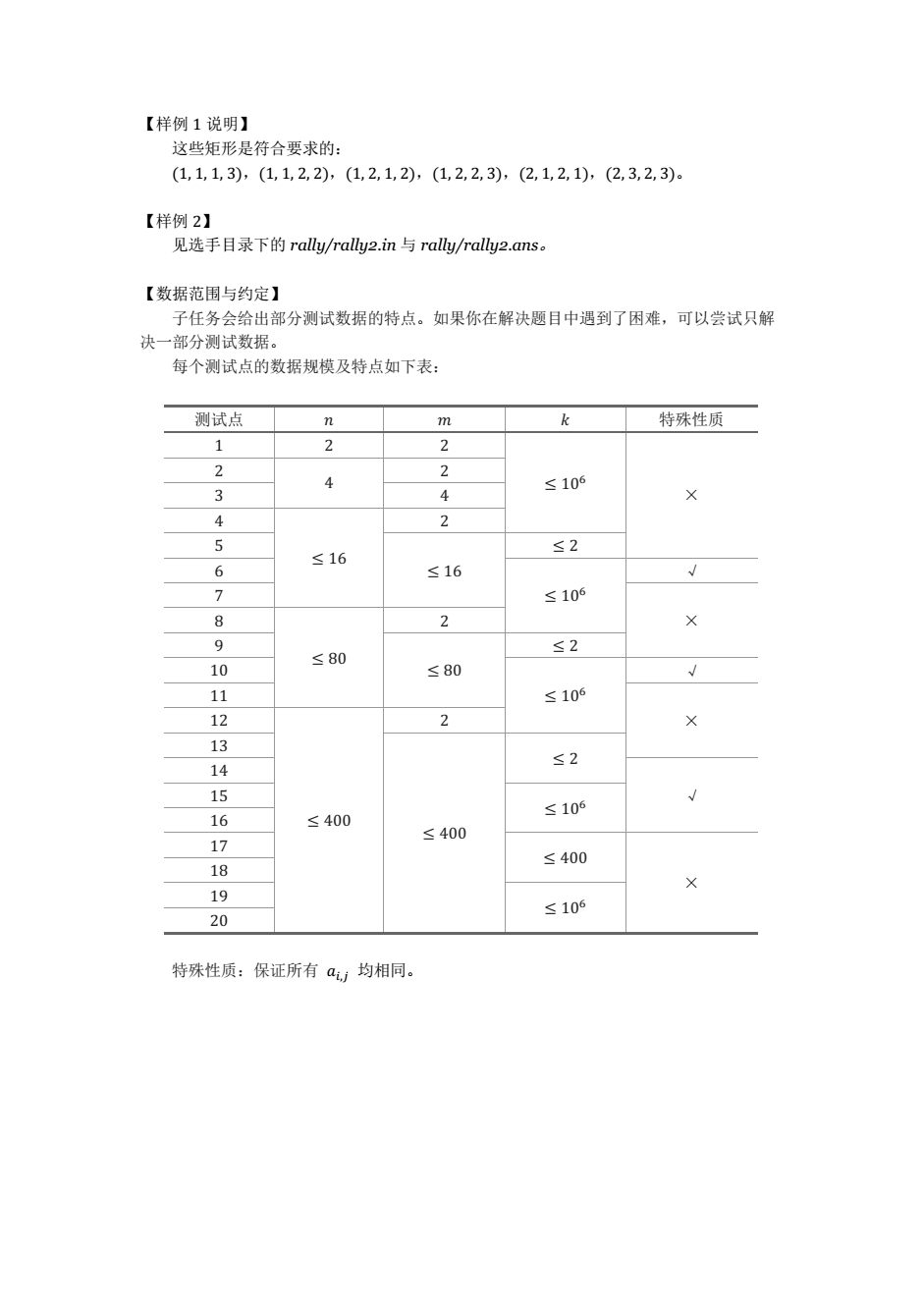
分析：其实很容易想到O(n^3m^3)的算法，枚举x1,x2,y1,y2,再统计一下和.求和可以用前缀和，能优化到O(n^2m^2),能得到60分.对于特殊性质的点，求一下a[i][j]与k的最小公倍数lcm,就可以推出来要选多少个点，乘法原理推一下就能解决了.

满分做法的思想是降维，先分析一下一维怎么做.问题要求满足(a[l] + a[l + 1] + ...... + a[r]) % k = 0的区间[l,r]有多少个.利用前缀和优化就是(sum[r] - sum[l - 1]) % k = 0.对约束进行变形:sum[r] % k = sum[l - 1] % k. O(n)的扫一遍，记录当前的sum[i] % k,看前面有多少个和它相同的就可以了.

转化到二维上，为了用上一维的做法，固定矩形的上边界和下边界，把每一列看做是一个元素a[i],就可以用上一维的做法了，是一个非常常见的变形.

求子矩阵问题的常用思路是先转化到1维上进行处理，再把行或列压一下，就能把2维放到1维上处理了，数学式子一定要会变形！

75分暴力：

#include <cmath>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long ll;

ll n, m, k, a[][], sum[][], t, ans;
bool flag = true;

void solve2()
{
    for (int i = ; i <= n; i++)
        for (int j = ; j <= m; j++)
            for (int p = i; p <= n; p++)
                for (int q = j; q <= m; q++)
                {
        ll temp = sum[p][q] - sum[i - ][q] - sum[p][j - ] + sum[i - ][j - ];
        if (temp % k == )
            ans++;
                }
    printf("%lld\n", ans);
}

ll gcd(ll a, ll b)
{
    if (!b)
        return a;
    return gcd(b, a % b);
}

void solve1()
{
    ll lcm = a[][] / gcd(a[][], k) * k;
    ll res = lcm / a[][];
    ll temp = ;
    while (res <= n * m)
    {
        temp = ;
        for (ll i = ; i <= n; i++)
            if (res % i ==  && (res / i) <= m)
                temp += (n - i + ) * (m - res / i + );
        //printf("%lld %lld\n", res, temp);
        ans += temp;
        res += lcm / a[][];
    }
    printf("%lld\n", ans);
}

int main()
{
    scanf("%lld%lld%lld", &n, &m, &k);
    for (int i = ; i <= n; i++)
        for (int j = ; j <= m; j++)
        {
        scanf("%lld", &a[i][j]);
        if (!(i ==  && j == ) && a[i][j] != t)
            flag = false;
        t = a[i][j];
        sum[i][j] = sum[i - ][j] + sum[i][j - ] - sum[i - ][j - ] + a[i][j];
        }
    if (flag)
        solve1();
    else
        solve2();

    return ;
}

正解：

#include <cmath>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long ll;

ll n, m, k, a[][], sum[][], ans, cnt[];

int main()
{
    scanf("%lld%lld%lld", &n, &m, &k);
    for (int i = ; i <= n; i++)
        for (int j = ; j <= m; j++)
        {
            scanf("%lld", &a[i][j]);
            sum[i][j] = sum[i - ][j] + sum[i][j - ] - sum[i - ][j - ] + a[i][j];
        }
    for (int i = ; i < n; i++)
        for (int j = i + ; j <= n; j++)
        {
            cnt[] = ;
            for (int kk = ; kk <= m; kk++)
            {
                ll p = (sum[j][kk] - sum[i][kk] + k) % k;
                ans += cnt[p];
                cnt[p]++;
            }
            for (int kk = ; kk <= m; kk++)
                cnt[(sum[j][kk] - sum[i][kk] + k) % k] = ;
        }
    printf("%lld\n", ans);

    return ;
}