Eureka 简介
Eureka 简介
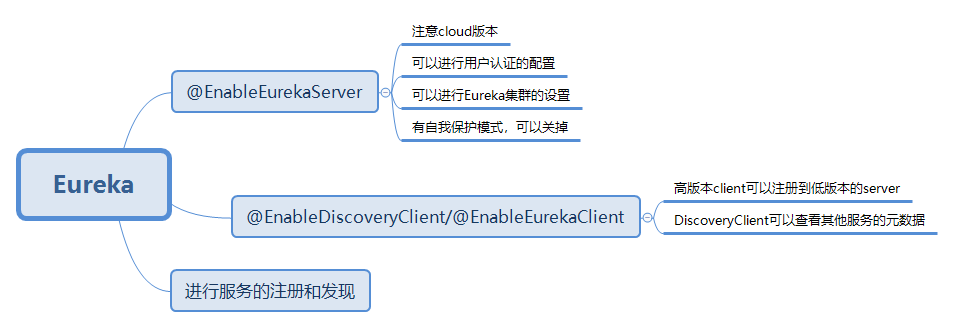
Eureka 简介的更多相关文章
- 微服务架构及Eureka简介
一.微服务架构 服务提供者.服务消费者.服务发现组件这三者之间的关系: 各个微服务在启动时,将自己的网络地址等信息注册到服务发现组件中,服务发现组件会存储这些信息. 服务消费者可从服务发现组件查询服务 ...
- 0401-服务注册与发现、Eureka简介
一.硬编码问题 解决方案:nginx.或.服务注册与发现 二.服务发现 注册.心跳机制 三.服务发现组件的功能 1.服务注册表:是一个记录当前可用服务实例的网络信息的数据库,是服务发现机制的核心.服务 ...
- 从零开始学spring cloud(三) -------- Eureka简介
1.服务发现组件:Eureka Eureka的开源文档介绍地址:https://github.com/Netflix/eureka/wiki/Eureka-at-a-glance What is Eu ...
- Spring Cloud Eureka简介及原理
Eureka是Netflix开发的服务发现组件,本身是一个基于REST的服务.Spring Cloud将它集成在其子项目spring-cloud-netflix中,以实现Spring Cloud的服务 ...
- Eureka简介
Eureka是Spring Cloud Netfix 的一个子模块,也是核心模块之一,用于云端服务发现.一个基于RestFul的服务,用于定位服务,以实现云端中间层服务发现和中间层转移. 服务注册与发 ...
- Spring Cloud Eureka 1(eureka简介)
Spring Cloud Eureka 是 Spring Cloud Netflix微服务套件中的一部分,基于netflix eureka做了二次封装,主要负责完成微服务架构中的服务治理功能. 服务治 ...
- Eureka 简介以及简单示例(创建EurekaServer工程)
Eureka 是一款开源的服务注册与发现组件,通过配合其他组件可提供负载均衡能力. 服务发现类型的技术对比: 名称 类型 AP/CP 语言 依赖 集成 一致性算法 Eureka General AP ...
- spring cloud之eureka简介
最近线上的接口出了一些问题,有一些可能不是代码的问题,但是由于是测试和其他方面的同事爆出来的,所以感觉对接口的监控应该提上日程. 经过搜索发现,spring cloud的eureka就是专门做这方面工 ...
- 服务注册与发现【Eureka】- Eureka简介
什么是服务治理 SpringCloud 封装了 Netflix 公司开发的 Eureka 模块来 实现服务治理. 在传统的rpc远程调用框架中,管理每个服务与服务之间依赖关系比较复杂,管理比较复杂,所 ...
随机推荐
- 网新恩普(W 笔试)
选择题 1.一桶有黄色,绿色,红色三种,闭上眼睛抓取同种颜色的两个.抓取多少个就可以确定你肯定有两个同一颜色的球? 答案: 4次 1.最坏打算抓3次都是不同颜色的黄.绿.红,此时,三种颜色的球各抓了一 ...
- docker 应用数据的管理之bind mounts
创建容器使用bind mounts 挂载文件系统.宿主机文件系统会覆盖掉容器里初始数据 [root@localhost ~]# mkdir /www/htpm -pv mkdir: 已创建目录 &qu ...
- 查看cuda版本和cudann
nvcc -V 没有找到直接查询cudann版本的命令,但发现cudann装在 /usr/local/cuda/lib64/目录下,libcudnn.so就是相应版本
- 最短路 || HDU 2066 一个人的旅行
本草的旅行故事(✺ω✺),可以从S个点中的任意一个开始,到达D个点中的任意一个,求最短路 *解法:把草儿的家记成点0,S个点与0的距离为0,然后spfa求最短路 又是改了一万次,①多组数据啊 ②改完多 ...
- 【转】C#中的==、Equal、ReferenceEqual
[转]C#中的==.Equal.ReferenceEqual 转载自: http://www.cnblogs.com/zagelover/articles/2741409.html 1. Refere ...
- web.config中配置数据库连接的两种方式
在ASP.NET中有两种配置数据库连接代码的方式,它们分别是 appSettings 和 connectionStrings .在使用 appSettings 和 connectionStrings ...
- OpenCV2:总结篇 工具方法函数
一.简介 OpenCV提供了一些工具方法函数来辅助完成图像运算 二.时间相关 1.getTickCount()和getTickFrequency() double tTime; tTime = (do ...
- 利用pyautogui自动化领取dnf的在线养竹活动的竹子
背景: Dnf的周年庆活动之一,鬼才策划为了在线率想的活动,规律如下 1.在线1分钟可以生成1根竹子,领取竹子以后可以获取到积分,积分满足活动要求后可以领取相应档位的奖励 2.玩家不在线期间,不会生成 ...
- No-4.文件和目录常用命令
文件和目录常用命令 结构 查看目录内容 ls 切换目录 cd 创建和删除操作 touch rm mkdir 拷贝和移动文件 cp mv 查看文件内容 cat more grep 其他 echo 重定向 ...
- react 语法细节总结说明
1.当要获取某个数据列表中的某个字段时,用“.”附加的形式.例如:获取user中的balance字段,用this.props.user.balance 来表示. 2.当要打印某个数据或字段结果时,co ...
