Milking Grid POJ - 2185 || 最小覆盖子串

Milking Grid POJ - 2185

最小覆盖子串：

最小覆盖子串（串尾多一小段时，用前缀覆盖）长度为n-next[n]（n-pre[n]），n为串长。

当n%(n-next[n])==0时，有最小循环节（就是最小覆盖子串）。

快照：

我对KMP的一些理解（lyp点拨的）：pre[i]（或next[i]）的实质是串str[1..i]的最长且小于i的“相等前、后缀”分别为str[1..pre[i]]（前缀）与str[(i-pre[i]+1)..i]（后缀），通俗讲就是：使str[1..i]前k个字母与后k个字母相等的最大k值。

KMP算法详解可见：http://blog.csdn.net/fjsd155/article/details/6864233

另外一个结论：

最小覆盖子串（串尾多一小段时，用前缀覆盖）长度为n-next[n]（n-pre[n]），n为串长。

证明分两部分：

１－长为n-next[n]的前缀必为覆盖子串。

当next[n]<n-next[n]时，如图a，长为next[n]的前缀A与长为next[n]的后缀B相等，故长为n-next[n]的前缀C必覆盖后缀B；

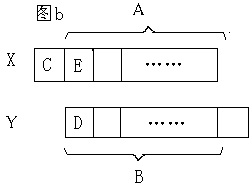
当next[n]>n-next[n]时，如图b，将原串X向后移n-next[n]个单位得到Y串，根据next的定义，知长为next[n]的后缀串A与长为前缀串B相等，X串中的长为n-next[n]的前缀C与Y串中的前缀D相等，而X串中的串E又与Y串中的D相等……可见X串中的长为n-next[n]的前缀C可覆盖全串。

２－长为n-next[n]的前缀是最短的。

如图c，串A是长为n-next[n]的前缀，串B是长为next[n]的后缀，假设存在长度小于n-next[n]的前缀C能覆盖全串，则将原串X截去前面一段C，得到新串Ｙ，则Ｙ必与原串长度大于next[n]的前缀相等，与next数组的定义（使str[1..i]前k个字母与后k个字母相等的最大k值。）矛盾。得证！有人问，为什么Ｙ与原串长大于next[n]的前缀相等？由假设知原串的构成必为CCC……E（E为C的前缀），串Ｙ的构成必为CC……E（比原串少一个Ｃ），懂了吧！

首先是这种情况：最长公共前缀后缀不重合

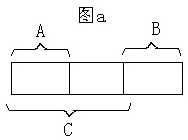
此时显然C串是覆盖子串（C能覆盖C；由于B和A相同而C覆盖A，C也能覆盖B）。为什么是最小的呢？

首先，此时A和B已经是最长的公共前缀后缀，也就是不可能使得公共前缀后缀有重合部分。假设有一个更小的覆盖子串D，那么D右侧的剩余部分E一定长于B，而由于D能覆盖E，E一定是D的开头一部分，E一定是公共前缀后缀，而E大于B，B却是最长的公共前缀后缀，矛盾。

然后是这种情况：最长公共前缀后缀重合

http://www.cnblogs.com/wuyiqi/archive/2012/01/06/2314078.html

http://www.cnblogs.com/chenxiwenruo/p/3546457.html

（端点到底算哪段并不影响）

两段红的为最长公共前缀后缀，表明s[k..j]==s[m..i]。

记s[a..b]为ab.

取x点使得x到j的长度等于j到i的长度，由于xj和ji分别是kj和mi最后的相同长度的一段，xj=ji。

那么kj=kx+xj, mi=mj+ji.

而kj=mi, xj=ji，因此kx=mj。

这一步由kj=mi得到了kx=mj和xj=ji。由kx=mj可以继续按原来的模型证下去，直到最长公共前缀后缀不重叠。可以发现这是一个递归/递推的证明过程。

例1：

ababababa

abababa
    abababa
123456789

17=15+67
39=37+89

67=89,17=39-->15=37

15=13+45
37=35+67

15=37,45=67-->13=35

13=1+23
35=3+45

13=35,23=45-->1=3

23=45=67=89,2=4=6=8,1=3=5=7=9,因此也可以视为12=34=56=78

例2：

abababab

ababab
    ababab
12345678

16=14+56
38=36+78

16=38,56=78-->14=36

14=12+34
36=34+56

14=36,34=56-->12=34

12=34=56=78

那么为什么是最小的覆盖子串呢？

http://blog.csdn.net/fjsd155/article/details/6866991

如图，根据前一步的证明，原串可以表示为ABABABABA

（A可能为空串，A、B连接起来（表示为AB）就是最小覆盖子串）

假设存在长度小于AB的前缀CD能覆盖全串，那么全串能表示为CDCD...CDC。则将原串X截去前面一段CD，得到新串Ｙ，那么Y能表示为CD...CDC（比全串少一个CD）。显然，Y是原串的公共前后缀，而且Y比原串去掉一个AB得到的公共前后缀要长（因为AB长于CD，相同长度的原串减去CD后的长度一定长于减去AB后的长度），这与原串去掉一个AB得到的公共前后缀是"最长公共前后缀"的条件矛盾。

这道题很容易想错，有一大堆错误题解。

错误方法：

求每行最小覆盖子串的lcm，就是宽度。

hack数据：

2 8
aaabcaaa
abababab
4 7
aaaaaaa
abababa
abcabca
abcdabc
2 12
abababababab
abcabcabcabc

正解：

http://poj.org/showmessage?message_id=153316

http://blog.csdn.net/maxmercer/article/details/76168361

http://www.cnblogs.com/chenxiwenruo/p/3549967.html

http://blog.sina.com.cn/s/blog_69c3f0410100tyjl.html

代码：

 #include<iostream>
 #include<cstring>
 #include<algorithm>
 #include<string>
 using namespace std;
 int ans_col[];//ans_col[i]表示0..i-1列可以覆盖整行的行的数量
 int f[],x;
 int ma_size;
 int r,c;//m=c
 string s[];
 bool cmp(int a,int b)
 {
     int i;
     for(i=;i<x;i++)
         if(s[a][i]!=s[b][i])
             return true;
     return false;
 }
 void getf(const string& s)
 {
     int i=,j=f[]=-;
     while(i<c)
     {
         while(j>=&&s[i]!=s[j])    j=f[j];
         i++;j++;
         f[i]=j;
     }
 }
 int getf2()
 {
     int i=,j=f[]=-;
     while(i<r)
     {
         while(j>=&&cmp(i,j))    j=f[j];
         i++;j++;
         f[i]=j;
     }
     return r-f[r];
 }
 void work(int i)
 {
     while(f[i]>=)
     {
         ans_col[c-f[i]]++;
         i=f[i];
     }
 }
 int main()
 {
     ios::sync_with_stdio(false);
     int i,t;
     cin>>r>>c;
     for(i=;i<r;i++)
     {
         cin>>s[i];
         getf(s[i]);
         work(c);
     }
     for(i=;i<=c;i++)
         if(ans_col[i]==r)
         {
             x=i;
             break;
         }
     //x就是最小的子矩阵列数
     cout<<getf2()*x;
     return ;
 }

曾经错误：f和row开小，只有80，导致WA。只比较每一行的前宽度个字符，但写成了比较整一行，似乎...并不会导致错误?

（map其实根本就没有用，把getf2里面的比较换成直接比较字符串（当然要先求出对应宽度的子串放进新字符串数组））

 #include<iostream>
 #include<cstring>
 #include<map>
 #include<algorithm>
 #include<string>
 using namespace std;
 map<string,int> ma;//其实根本就没有用
 int ans_col[];//ans_col[i]表示0..i-1列可以覆盖整行的行的数量
 int f[],x;
 int row[],ma_size;
 int r,c;//m=c
 string s[];
 void getf(const string& s)
 {
     int i=,j=f[]=-;
     while(i<c)
     {
         while(j>=&&s[i]!=s[j])    j=f[j];
         i++;j++;
         f[i]=j;
     }
     //return m-f[m];
 }
 int getf2()
 {
     int i=,j=f[]=-;
     while(i<r)
     {
         while(j>=&&row[i]!=row[j])    j=f[j];
         i++;j++;
         f[i]=j;
     }
     return r-f[r];
 }
 //void work(int i)
 //{
 //    if(f[i]>=0)    work(f[i]),ans_col[m-f[i]]++;
 //}
 void work(int i)
 {
     while(f[i]>=)
     {
         ans_col[c-f[i]]++;
         i=f[i];
     }
 }
 int main()
 {
     ios::sync_with_stdio(false);
     int i,t;
     cin>>r>>c;
     for(i=;i<r;i++)
     {
         cin>>s[i];
         getf(s[i]);
         work(c);
     }
     for(i=;i<=c;i++)
         if(ans_col[i]==r)
         {
             x=i;
             break;
         }
     //x就是最小的子矩阵列数
     for(i=;i<r;i++)
         if(ma.count(s[i])==)
         {
             row[i]=ma_size;
             ma[s[i]]=ma_size++;
         }
         else
             row[i]=ma[s[i]];
     cout<<getf2()*x;
     return ;
 }