[Comet OJ - Contest #7 D][52D 2417]机器学习题_斜率优化dp

机器学习题

题目大意：

数据范围：

---

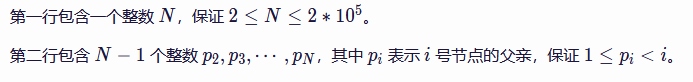
题解：

学长说是决策单调性？

直接斜率优化就好了嘛

首先发现的是，$A$和$B$的值必定是某两个$x$值。

那么我们就把，$y$的正负分成两个序列，$val1_i$表示$A$取序列中第$i$个数的值是，给的代价，$val2_i$同理。

那么最终的答案情况就是一个$i$一个$j$，分别是$val1_i + val2_j + a_i.x^2 + b_j.x^2 - 2*a_i.x\times b_j.x$。

显然可以斜率优化。

把第一个数列里的所有数抽象成点，为$(-2*a_i.x , val1_i + a_i.x^2)$。

弄一个下凸包，$B$递增枚举然后在凸包上切就好了。

但是，由于我们有一步排序，所以复杂度是$O(nlogn)$。

代码：

#include<bits/stdc++.h>

#define N 500010 

using namespace std;

typedef long long ll;

ll bfr[N], aft[N], g[N], f[N], ans = 1e18;

int n, head, tail, m, x[N], y[N], id[N], p[N], q[N], b[N];

char *p1, *p2, buf[100000];

#define nc() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1 ++ )

int rd() {
	int x = 0, f = 1;
	char c = nc();
	while (c < 48) {
		if (c == '-')
			f = -1;
		c = nc();
	}
	while (c > 47) {
		x = (((x << 2) + x) << 1) + (c ^ 48), c = nc();
	}
	return x * f;
}

inline double slove(int i, int j) {
	return 1.0 * (g[i] - g[j]) / (p[i] - p[j]);
}

inline ll sqr(int x) {
	return 1ll * x * x;
}

int main() {
	n = rd();
	for (int i = 1; i <= n; i ++ )
		b[i] = x[i] = rd(), y[i] = rd();
	sort(b + 1, b + n + 1);
	m = unique(b + 1, b + n + 1) - b - 1;
	p[1] = b[1] - 1;
	p[m + 2] = b[m] + 1;
	for (int i = 1; i <= m; i ++ )
		p[i + 1] = b[i];
	for (int i = 1, k; i <= n; i ++ ) {
		k = lower_bound(b + 1, b + m + 1, x[i])  -b;
		bfr[k + 1] += max(-y[i], 0);
		aft[k + 1] += max(y[i], 0);
	}
	n = m + 2;
	for (int i = 1; i <= n; i ++ )
		bfr[i] += bfr[i - 1];
	for (int i = n; i; i -- )
		aft[i] += aft[i + 1];
	for (int i = 1; i <= n; i ++ )
		g[i] = bfr[i - 1] + sqr(p[i]);
	head = 1, tail = 0;
	for (int i = 1; i <= n; i ++ ) {
		while (head < tail && slove(q[tail - 1], q[tail]) >= slove(q[tail - 1], i))
			tail -- ;
		q[ ++ tail] = i;
		while (head < tail && slove(q[head], q[head + 1]) <= 2 * p[i])
			head ++ ;
		f[i] = sqr(p[i] - p[q[head]]) + bfr[q[head] - 1] + aft[i + 1];
		ans = min(ans, f[i]);
	}
	cout << ans << endl ;
	return 0;
}

小结：形式比较明显，斜率优化非常显然。还是要学一下决策单调性才行.....