数据结构图之三（最短路径--迪杰斯特拉算法——转载自i=i++

数据结构图之三（最短路径--迪杰斯特拉算法）

 

【1】最短路径

最短路径？别乱想哈，其实就是字面意思，一个带边值的图中从某一个顶点到另外一个顶点的最短路径。

官方定义：对于内网图而言，最短路径是指两顶点之间经过的边上权值之和最小的路径。

并且我们称路径上的第一个顶点为源点，最后一个顶点为终点。

由于非内网图没有边上的权值，所谓的最短路径其实是指两顶点之间经过的边数最少的路径。

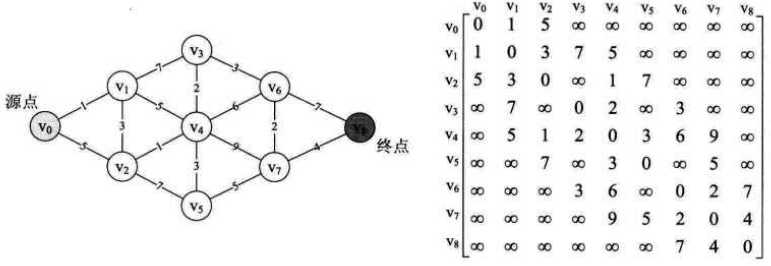
别废话了！整点实际的哈，你能很快计算出下图中由源点V0到终点V8的最短路径吗？

【2】迪杰斯特拉算法

迪杰斯特拉算法是按路径长度递增的次序产生最短路径的思路求解。

具体算法及其详细讲解如下：

阅读程序前，先要搞明白几个数组作用：

final[w]=1; 表示V0到Vw顶点已经有最短路径的结果

ShortPathTable[w]; 表示V0到Vw顶点的最短路径权值和

Pathmatirx[w]; 表示V0到Vw顶点的前驱顶点下标值

开始调用算法前，我们需要为案例图创建邻接矩阵图，如下所示：

（1）程序开始运行，final数组是为了标记V0到某顶点是否已经求得最短路径。

　　如果V0到Vw已经有结果，那么final[w]=1;

（2）第5~10行，是对数据初始化工作。 此时final数组均赋值为0，表示所有点均未求得最短路径。

　　D数组为 {0,1,5,65515,65535,65535,65535,65535,65535}。因为V0与V1和V2的边权值为1和5。

　　P数组全为0，表示目前没有路径。

（3）第11行，表示V0至V0路径为0。

　　第12行，表示V0点到V0点已经求得最短路径，因此final[0]=1。

　　此时final数组为 {1,0,0,0,0,0,0,0,0}，此时整个初始化工作完成。

（4）第13~33行为主循环，每次循环求得V0与一个顶点的最短路径。除去V0，因此索引从1开始。

（5）第15~23行，先令min为65535的极大值，通过w控制循环，与D[w]比较找到最小值为min=1，同时确定k=1。

（6）第24行，由k=1可知与V0最近的顶点是V1，并且由D[1]=1知道此时V0到V1的最短路径是1。

　　因此再将对应的final[1]设置为1。此时final数组为 {1,1,0,0,0,0,0,0,0}

（7）第25~32行是一循环，此循环甚为关键。

　　它的目的是在刚才已经找到V0与V1的最短路径基础之上，对V1与其它顶点的边进行计算，得到V0与它们的当前最短距离，如图所示：

　　因为min=1,所以D[2]=5不再是V0到V2的最短路径，现在D[2]=V0->V1->V2=min+3=4, D[3]=V0->V1->V3=min+7=8,

　　D[4]=V0->V1->V4=min+5=6，于是D数组当前值为 {0,1,4,8,6,65535,65535,65535,65535}。

　　而P[2]=1，P[3]=1，P[4]=1，其表示V0到V2，V3，V4点的最短路径它们的前驱均是V1。

　　此时P数组为 {0,0,1,1,1,0,0,0,0}。

（8）新一轮循环，此时i=2。第15~23行，对w循环，注意因为final[0]=1和final[1]=1，由第18行的！final[w]可知：

　　V0与V1并不参与最小值的获取。通过循环比较，找到最小值min=4，k=2。

（9）第24行，由k=2，表示已经求出V0到V2的最短路径，并且由D[2]=4知道最短路径距离为4。

　　因此将V2对应的final[2]设置为1，此时final数组为 {1,1,1,0,0,0,0,0,0}。

（10）第25~32行，在刚才已经找到V0与V2的最短路径的基础上，对V2与其它顶点的边进行计算，得到V0与它们的最短距离。

　　如图所示：

　　因为min=4，所以D[4]=6不再是V0到V4的最短距离，现在D[4]=V0->V2->V4=min+1=5，D[5]=V0->V2->V5=min+7=11。

　　因此D数组当前值为 {0,1,4,8,5,11,65535,65535,65535,65535}。

　　而原本P[4]=1，此时P[4]=2，P[5]=2，它表示的意思是V0到V4和V5的最短路径前驱均为V2。

　　此时P数组为 {0,0,1,1,2,2,0,0,0}。

（11）重新再开始一轮循环，此时i=3。第15~23行，通过对w循环比较找到最小值min=5，k=4。

（12）第24行，由k=4表示已经求出V0到V4的最短路径，并且由D[4]=5知道最短路径距离为5。

　　因此将V4对应的final[4]设置为1。此时final数组为 {1,1,1,0,1,0,0,0,0}。

（13）第25~32行，对V4与其它顶点的边值进行计算，得到V0与它们的当前最短距离，如图所示：

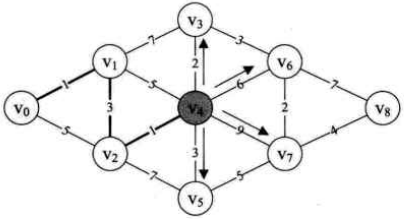
　　因为min=5，所以D[3]=8不再是V0到V3的最短路径，现在D[3]=V0->V4->V3=min+2=7，同理：

　　D[5]=V0->V4->V5=min+3=8，D[6]=V0->V4->V6=min+6=11，

　　D[7]=V0->V4->V7=min+9=14，因此，D数组当前值为 {0,1,4,7,5,8,11,14,65535}。

　　而原本P[3]=1，此时P[3]=4，原本P[5]=2，此时P[5]=4。

　　另外P[6]，P[7]=4，它表示V0到V3，V5，V6，V7点的最短路径它们的前驱是V4。

　　此时P数组值为 {0,0,1,4,2,4,4,4,0}。

（14）之后的循环完全类似。得到最终的结果，如图所示：

　　此时final数组为 {1,1,1,1,1,1,1,1,1}，它表示所有的顶点均完成了最短路径的查找工作。

　　此时D数组为 {0,1,4,7,5,8,10,12,16}，它表示V0到各个顶点的最短路径数，比如D[8]=1+3+1+2+3+2+4=16。

　　此时的P数组为 {0,0,1,4,2,4,3,6,7}：

　　这个P数组值可能难理解一些。比如P[8]=7，它表示要查看V0到V8的最短路径时，顶点V8的前驱是V7；

　　再由P[7]=6表示要查看V0到V7的最短路径时，顶点V7的前驱是V6，同理，P[6]=3表示V6的前驱是V3。

　　这样就可以得到：V0到V8最短路径为V8<-V7<-V6<-V3<-V4<-V2<-V1<-V0

　　即就是： V0->V1->V2->V4->V3->V6->V7->V8。

【3】算法实现

实现代码如下：

 #include <iostream>
 #include "SeqList.h"
 #include "Stack.h"
 #include <iomanip>
 using namespace std;

 #define  INFINITY  65535

 template<class NameType, class DistType>
 class Graph
 {
 private:
     SeqList<NameType> Vertices;
     DistType **Edges;
     int nVer, nEdges;

 public:
     Graph()
         : Edges(NULL)
         , nEdges()
         , nVer()
     {}
     ~Graph()
     {}

 public:
     int GetVer() const
     {
         return nVer;
     }

     istream & operator>>(istream &in)
     {
         int v, u, value;
         int i, j;
         NameType item;
         cout << "请输入顶点的个数: " << endl;
         in >> nVer;
         cout << "请输入顶点的数据信息: " << endl;
         for (i = ; i < nVer; ++i)
         {
             in >> item;
             Vertices.push_back(item);    // 保存全部顶点
         }
         /////二维数组的创建并初始化
         Edges = new DistType*[nVer]; // DistType *ar[10];
         for (i = ; i < nVer; ++i)
         {
             Edges[i] = new DistType[nVer];
             for (j = ; j < nVer; ++j)
             {
                 Edges[i][j] = ;
             }
         }
         cout << "请输入边的个数: " << endl;
         in >> nEdges;
         cout << "请输入边的信息：" << endl;
         for (i = ; i < nEdges; ++i)
         {
             in >> v >> u >> value;
             Edges[v][u] = value;
             Edges[u][v] = value;
         }
         return in;
     }
     ostream & operator<<(ostream &out) const
     {
         int i, j;
         out << "顶点信息 " << endl;
         for (i = ; i <= nVer; ++i)
         {
             out << Vertices[i] << setw();
         }
         out << endl;
         out << "矩阵信息：" << endl;
         out << setw();
         for (i = ; i <= nVer; ++i)
         {
             out << Vertices[i] << setw();
         }
         out << endl;
         for (i = ; i < nVer; ++i)
         {
             out << Vertices[i+] << setw();
             for (j = ; j < nVer; ++j)
             {
                 if ( == Edges[i][j] && i != j)
                     Edges[i][j] = INFINITY;
                 cout << Edges[i][j] << setw();
             }
             out << endl;
         }
         out << endl;

         return out;
     }
     // 迪杰斯特拉算法实现
     void ShortestPath_Dijkstra(int v0, int* final, int*p, int *D)
     {
         int v, w, k, min;
         // 初始化数据
         for (v = ; v < nVer; ++v)
         {
             final[v] = ;    // 全部顶点初始化为未知对短路径状态
             D[v] = Edges[v0][v]; //将与V0点有连线的顶点加上权值
             p[v] = ;    // 初始化路径数组p为0
         }
         D[v0] = ;    // V0至V0路径为0
         final[v0] = ;    // final[W]=1表示V0至V0不需要求路径
         // 开始主循环，每次求得V0到某个V顶点的最短路径
         for (v = ; v < nVer; ++v)
         {
             min = INFINITY;    // 当前所知离V0顶点最近距离
             for (w = ; w < nVer; ++w) // 寻找离V0最近的顶点
             {
                 if (!final[w] && D[w] < min)
                 {
                     min = D[w]; // w顶点离V0顶点更近
                     k = w;
                 }
             }

             final[k] = ; // 将目前找到的最近的顶点置为1
             for (w = ; w < nVer; ++w) // 修正当前最短路径距离
             {
                 // 如果经过V顶点的路径比现在这条路径的长度短的话
                 if (!final[w] && (min + Edges[k][w] < D[w]))
                 {
                     // 说明找到了最短的路径，修改D[w] 和 p[w]
                     D[w] = min + Edges[k][w]; // 修改当前路径长度
                     p[w] = k;
                 }
             }
         }
     }
 };

 template<class NameType, class DistType>
 istream & operator>>(istream &in, Graph<NameType,DistType> &g)
 {
     g >> in;
     return in;
 }

 template<class NameType, class DistType>
 ostream & operator<<(ostream &out, const Graph<NameType,DistType> &g)
 {
     g << out;
     return out;
 }

 void main()
 {
     Graph<char, int> myg;
     cin >> myg;
     cout << "打印所有输入信息：" << endl;
     cout << myg << endl;
     cout << "求最短路径....." << endl;
     int numVer = myg.GetVer();
     int* pFinal = new int[numVer];
     int* pPathmatirx = new int[numVer];
     int* pShortPath = new int[numVer];
     myg.ShortestPath_Dijkstra(, pFinal, pPathmatirx, pShortPath);
     cout << "打印各顶点最短路径标记数组值：" << " ";
     for (int i = ; i < numVer; ++i)
     {
         cout << pFinal[i] << " ";
     }
     cout << endl;
     cout << "打印最短路径数组值：" << " ";
     for (int i = ; i < numVer; ++i)
     {
         cout << pShortPath[i] << " ";
     }
     cout << endl;
     cout << "打印最短路径前驱数组值：" << " ";
     for (int i = ; i < numVer; ++i)
     {
         cout << pPathmatirx[i] << " ";
     }
     cout << endl;
     cout << "打印V0到各个顶点最短路径值以及路径信息：" << endl;
     SeqStack<int> sQ;
     for (int i = ; i < numVer; ++i)
     {
         cout << "V0~V" << i << ": " << pShortPath[i] << endl;

         sQ.Push(pPathmatirx[i]);
         int n = ;
         while (sQ.GetTop(n) && n != )
         {
             sQ.Push(pPathmatirx[n]);
         }

         while (!sQ.IsEmpty())
         {
             int m = ;
             sQ.Pop(m);
             cout << "V" << m << "->";
         }
         cout << "V" << i << endl;
     }
     delete []pFinal;
     delete []pPathmatirx;
     delete []pShortPath;
     pFinal = NULL;
     pPathmatirx = NULL;
     pShortPath = NULL;
 }
 // 备注：
 // 最短路径迪杰斯特拉算法实现
 // 整理于2013-12-04
 // 测试输入程序为：
 /*
 请输入顶点的个数:
 9
 请输入顶点的数据信息:
 A B C D E F G H I
 请输入边的个数:
 16
 请输入边的信息：
 0 1 1
 0 2 5
 1 2 3
 1 3 7
 1 4 5
 2 4 1
 2 5 7
 3 4 2
 3 6 3
 4 5 3
 4 6 6
 4 7 9
 5 7 5
 6 7 2
 6 8 7
 7 8 4
 打印所有输入信息：
 顶点信息
 A    B    C    D    E    F    G    H    I
 矩阵信息：
 A    B    C    D    E    F    G    H    I
 A    0    1    5655356553565535655356553565535
 B    1    0    3    7    565535655356553565535
 C    5    3    065535    1    7655356553565535
 D65535    765535    0    265535    36553565535
 E65535    5    1    2    0    3    6    965535
 F6553565535    765535    3    065535    565535
 G655356553565535    3    665535    0    2    7
 H65535655356553565535    9    5    2    0    4
 I655356553565535655356553565535    7    4    0

 求最短路径.....
 打印各顶点最短路径标记数组值： 1 1 1 1 1 1 1 1 1
 打印最短路径数组值： 0 1 4 7 5 8 10 12 16
 打印最短路径前驱数组值： 0 0 1 4 2 4 3 6 7
 打印V0到各个顶点最短路径值以及路径信息：
 V0~V1: 1
 V0->V1
 V0~V2: 4
 V0->V1->V2
 V0~V3: 7
 V0->V1->V2->V4->V3
 V0~V4: 5
 V0->V1->V2->V4
 V0~V5: 8
 V0->V1->V2->V4->V5
 V0~V6: 10
 V0->V1->V2->V4->V3->V6
 V0~V7: 12
 V0->V1->V2->V4->V3->V6->V7
 V0~V8: 16
 V0->V1->V2->V4->V3->V6->V7->V8
  */

关于实现代码中的SeqList.h文件和Stack.h文件从随笔《顺序表》和《栈》中查找拷贝一份即可。调试环境为VS2010。

Good  Good  Study, Day  Day Up.

顺序  选择  循环  总结

 

转载自i=i++的博客