【算法学习笔记】RMQ问题与ST表

\(0.\) RMQ问题

P1816

人话翻译

给定一个长度为\(n\)的数列\(a\)，然后有\(m\)组询问，每次询问一个区间\([l,r]\)的最小值。

其中\(m,n\leq10^5\)

\(1.\) 暴力做法

很显然，暴力做法就是便历 \(\max\limits_{l\leq i\leq r}a_i\) 。这个做法最坏时间复杂度将会高达\(O(n^2)\)。很显然，这对于\(1e5\)的数据范围要炸

\(2.\) 正解

线段树

如果不知道什么是线段树，请点击这里 线段树

对于这种区间信息，线段树显然是能够维护的。但鉴于本题没有区间修改，线段树显然有点大材小用，并且数组模拟的线段树空间将会达到\(O(4n)\)

线段树还有一些缺点，就是它的查询时间复杂度最坏是\(O(logn)\)的，因为没有区间修改，这个时间开销也略微有点大。

\(ST\)表(倍增)

倍增算法的含义就是成倍增长。我们考虑一个这样的数据结构：

一个二维数组\(st\)，其中

\[st_{i,j}=\min\limits_{i\leq k\leq i+2^j}a_k
\]

我们假设一个数据：\(9\ 3\ 1\ 7\ 5\ 6\ 0\ 8\)

可以建立如下所示的\(ST\)表：

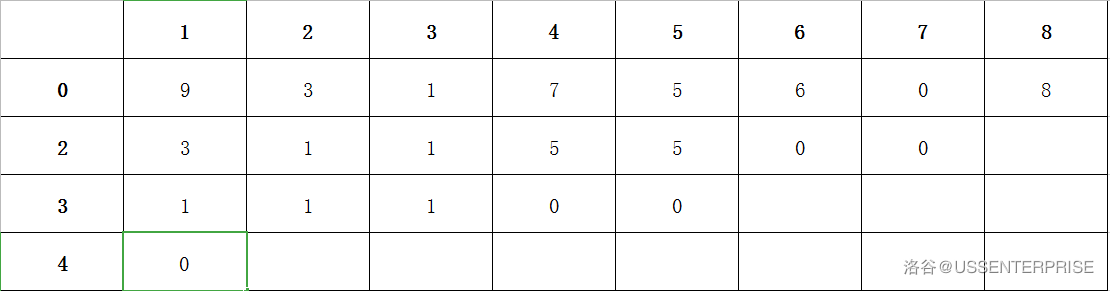
建表

我们发现，我们可以一层层地建表。这样，我们就可以通过递推，利用上层的信息，建表。

我们先将读入数据存在\(0\)这一行。

我们发现，要想实现建立这个表，我们需要每次倍增长度。而最简单的倍增长度方法就是将两段不相交的区间合并起来。

所以我们可以得到如下公式：

\[st_{i,j}=min(st_{i,j-1},st_{i+2^{j-1},j-1}
\]

这样，我们就能完成建表

for(rg int i=1;i<=16;i++){ // 由计算器可得 log1e5 约为 17，但是这里循环16次已经够了。
	for(rg int j=1;j+(1<<i)-1<=n;j++){
		st[i][j]=min(st[i-1][j],st[i-1][j+(1<<(i-1))]);
	}
}

• 注：为了方便，我们常常把这个表“竖”过来。本篇中的代码一律如此

我们可以发现，建表的时间复杂度是\(O(nlogn)\)的

查询

我们由上表知道，想要查询\([l,r]\)的最值，只需求出

\[min(st_{l,log(len)},st_{r-2^{log(len)+1},log(len)})
\]

其中

\[len=r-l+1
\]

比如上方的数据，我们想要查询\([3,8]\)

我们只需要从\(3\)往后\(4\)个，\(8\) 往前\(4\)个，肯定能够完全覆盖这个区间

所以我们的查询开销是\(O(1)\)的

ans=min(st[(int)log2(len)][l],st[(int)log2(len)][r-(1<<((int)log2(len)))+1]);

至此，我们已经完成了全部内容