Python验证数据的抽样分布类型

假如要对一份统计数据进行分析，一般其来源来自于社会调研/普查，所以数据不是总体而是一定程度的抽样。对于抽样数据的分析，就可以结合上篇统计量及其抽样分布的内容，判断数据符合哪种分布。使用已知分布特性，可以完成对总体的统计分析。

本文使用python函数判断数据集是否符合特定抽样分布。

数据来源

本次试验使用kagglehttps://www.kaggle.com/datasets上的公开数据集，可以通过搜索框进行数据集搜索。

通过搜索「income」关键值，最后决定使用https://www.kaggle.com/goldenoakresearch/us-household-income-stats-geo-locations/version/1#US_Income_Kaggle.csv这个数据集，其中包含抽样区域的家庭收入均值，中位数和标准差。通过页面中的pdf文件链接，可以获取每个字段的说明。

抽样分布验证

读入数据

import pandas as pd

import numpy as np

us_income = pd.read_csv("US_Income_Kaggle.csv", encoding="ISO-8859-1")

需要注意，csv文件的编码是Latin-1，因此需要显式指定编码读取。

画出收入均值的直方图

import seaborn as sns

sns.distplot(us_income['Mean'], color="b", bins=10, kde=True)

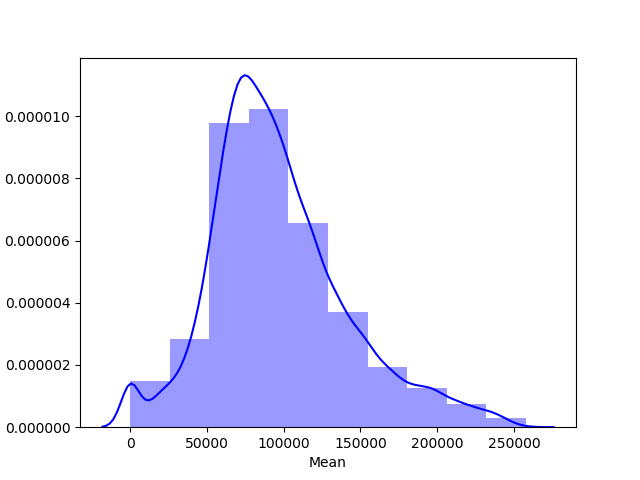
从图形看，在低收入侧，有一个数量的下降，并不符合正态分布的曲线。

使用函数判断是否服从正态分布

from scipy import stats

stats.kstest(us_income['Mean'], 'norm')

Out[23]: KstestResult(statistic=0.980404837353683, pvalue=0.0)

因为kstest可以做多种分布的验证，这里需要指定验证的分布类型为正态分布，即第2个参数。

stats.shapiro(us_income['Mean'])

UserWarning: p-value may not be accurate for N > 5000.

  warnings.warn("p-value may not be accurate for N > 5000.")

Out[25]: (0.9653068780899048, 0.0)

shapiro函数不适合样本数>5000的正态分布检验，所以这里提示warning。

stats.normaltest(us_income['Mean'],axis=0)

Out[27]: NormaltestResult(statistic=1170.1750576510913, pvalue=7.938067739808798e-255)

normaltest函数专门用于正态分布分布检验，其中axis=0表示按行读取数据。

通过以上的函数，可以得到所有的pvalue都小于0.05，这种情况下，我们认为区域收入平均值不服从正态分布。

是否服从t分布

np.random.seed(1)

ks = stats.t.fit(us_income['Mean'])

df = ks[0]

loc = ks[1]

scale = ks[2]

t_estm = stats.t.rvs(df=df, loc=loc, scale=scale, size=len(us_income['Mean']))

stats.ks_2samp(us_income['Mean'], t_estm)

Out[40]: Ks_2sampResult(statistic=0.07327168078639335, pvalue=1.7671996893936462e-36)

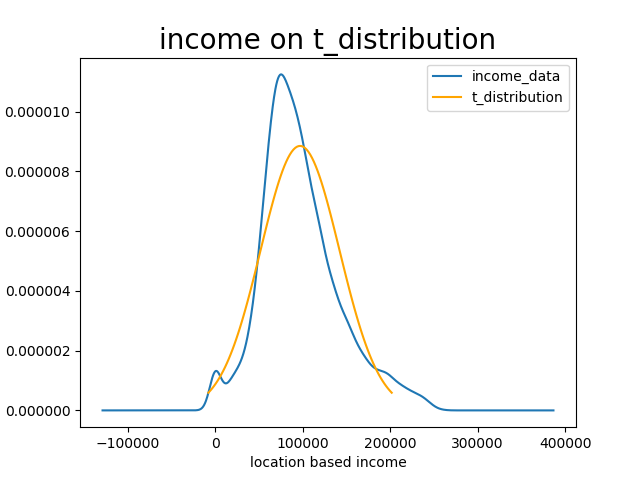
这里的思路是先用t分布拟合区域收入均值，然后使用ks_2samp函数比较区域收入均值和t分布的随机变量。因为pvalue小于0.05，认为该数据集不服从t分布。用以下方法可以画出拟合数据和数据集的对比图。

from matplotlib import pyplot as plt

plt.figure()

us_income['Mean'].plot(kind = 'kde')

t_distribution = stats.t(ks[0], ks[1],ks[2])

x = np.linspace(t_distribution.ppf(0.01), t_distribution.ppf(0.99), 100)

plt.plot(x, t_distribution.pdf(x), c='orange')

plt.xlabel('location based income')

plt.title('income on t_distribution', size=20)

plt.legend(['income_data', 't_distribution'])

是否服从卡方分布

np.random.seed(1)

chi_square = stats.chi2.fit(us_income['Mean'])

df = chi_square[0]

loc = chi_square[1]

scale = chi_square[2]

chi_estm = stats.chi2.rvs(df=df, loc=loc, scale=scale, size=len(us_income['Mean']))

stats.ks_2samp(us_income['Mean'], chi_estm)

Out[40]: Ks_2sampResult(statistic=0.07327168078639335, pvalue=1.7671996893936462e-36)

同样采用拟合值与原数据集比较，pvalue小于0.05，认为该数据不服从卡方分布。拟合数据和数据集的对比图方法同上，此处从略。

总结

对于数据集的抽样分布类型，可以使用scipy.stats包中的相应函数进行判断。其中，正态分布可以使用kstest，normaltest等函数；对于t分布和卡方分布，可以先对数据进行相应分布的拟合，然后用ks_2samp函数对拟合的数据同原始数据比较，获得两个数据是否服从相同的分布。

欢迎扫描二维码进行关注