隐马尔可夫模型HMM(二)概率计算问题
摘自
1.李航的《统计学习方法》
2.http://www.cnblogs.com/pinard/p/6955871.html
一、概率计算问题
上一篇介绍了概率计算问题是给定了λ(A,B,π),计算一个观测序列O出现的概率,即求P(O|λ)。
用三种方法,直接计算法,前向算法,后向算法。
考虑隐马尔可夫模型(一)中的盒子球模型。
假设Q={1,2,3,4}, V = {红,白},在给定λ(A,B,π)的条件下,其中:
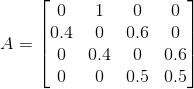 ,
, 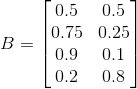 ,
,

求O=(红,白,红)的概率。
二、直接计算法
说通俗一点,就是暴力求解,穷举法。
- 所有可能的状态序列I,则状态序列I的概率为P(I|λ)
- 对于固定的状态序列I,则观测序列为O的概率P(O|I,λ)
- 联合概率为P(O,I|λ) = P(O|I,λ)P(I|λ)
- 则最后所求为P(O|λ) = ΣP(O|I,λ)P(I|λ)
状态集合有N个,一共有T个状态序列,所以状态序列的可能性为NT,每一种状态序列都要相应乘以T个观测概率矩阵,所以最后的时间复杂度为O(TNT)。
三、前向计算法
记αi(j)为部分观测序列为o1.....ot切ot状态为qj的概率。
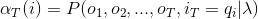
首先,记alphai(j)为第i次观测下状态为j,观测值为O(i)的概率,bj(i)为j状态下观测值为O(i)的概率, 暂时记i=1为红球,i=2为白球, aij为矩阵A中i行j列。
1、第一次观测为红球
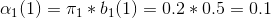


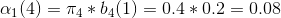
2、第二次观测为白球

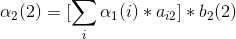
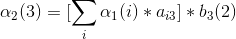
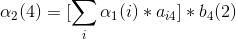
3、第三次观测
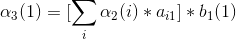
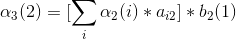
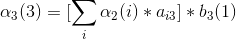
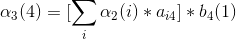
4、最后结果
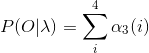
四、后向计算方法
βt(i)为On, On-1.... Ot观测序列且在Ot时刻状态为qi的概率:
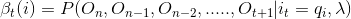
五、总结
根据前向传播算法,可以得到一些相关概率和期望。
1、给定模型输入λ和观测O,在时刻t处于状态qi 的概率为γt(i)。
(1)记γt(i):
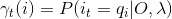
(2)由前向概率和后向概率表达式α和β可得:
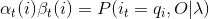
(3)因此:

(4)因此得到γt(i)
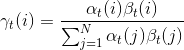
2、给定模型λ和观测O,在时刻t处于状态qi,且在时刻t+1处于状态qj的概率为εt(i, j)。
(1)记εt(i, j):
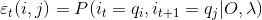
(2)通过前向后向计算可以得到:

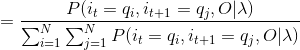
(3)由于:
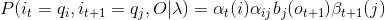
(4)因此:
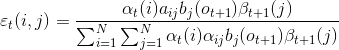
3、在观测O下由状态i出现的期望值:

4、在观测O下由状态i转移的期望值
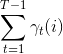
5、在观测O下由状态i转移到状态j的期望值:
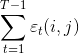
隐马尔可夫模型HMM(二)概率计算问题的更多相关文章
- 隐马尔科夫模型HMM(二)前向后向算法评估观察序列概率
隐马尔科夫模型HMM(一)HMM模型 隐马尔科夫模型HMM(二)前向后向算法评估观察序列概率 隐马尔科夫模型HMM(三)鲍姆-韦尔奇算法求解HMM参数(TODO) 隐马尔科夫模型HMM(四)维特比算法 ...
- 隐马尔可夫模型HMM与维特比Veterbi算法(二)
隐马尔可夫模型HMM与维特比Veterbi算法(二) 主要内容: 前向算法(Forward Algorithm) 穷举搜索( Exhaustive search for solution) 使用递归降 ...
- 隐马尔科夫模型HMM学习最佳范例
谷歌路过这个专门介绍HMM及其相关算法的主页:http://rrurl.cn/vAgKhh 里面图文并茂动感十足,写得通俗易懂,可以说是介绍HMM很好的范例了.一个名为52nlp的博主(google ...
- 猪猪的机器学习笔记(十七)隐马尔科夫模型HMM
隐马尔科夫模型HMM 作者:樱花猪 摘要: 本文为七月算法(julyedu.com)12月机器学习第十七次课在线笔记.隐马尔可夫模型(Hidden Markov Model,HMM)是统计模型,它用来 ...
- 隐马尔科夫模型HMM(一)HMM模型
隐马尔科夫模型HMM(一)HMM模型基础 隐马尔科夫模型HMM(二)前向后向算法评估观察序列概率 隐马尔科夫模型HMM(三)鲍姆-韦尔奇算法求解HMM参数(TODO) 隐马尔科夫模型HMM(四)维特比 ...
- 隐马尔科夫模型HMM(三)鲍姆-韦尔奇算法求解HMM参数
隐马尔科夫模型HMM(一)HMM模型 隐马尔科夫模型HMM(二)前向后向算法评估观察序列概率 隐马尔科夫模型HMM(三)鲍姆-韦尔奇算法求解HMM参数(TODO) 隐马尔科夫模型HMM(四)维特比算法 ...
- 隐马尔科夫模型HMM(四)维特比算法解码隐藏状态序列
隐马尔科夫模型HMM(一)HMM模型 隐马尔科夫模型HMM(二)前向后向算法评估观察序列概率 隐马尔科夫模型HMM(三)鲍姆-韦尔奇算法求解HMM参数 隐马尔科夫模型HMM(四)维特比算法解码隐藏状态 ...
- 用hmmlearn学习隐马尔科夫模型HMM
在之前的HMM系列中,我们对隐马尔科夫模型HMM的原理以及三个问题的求解方法做了总结.本文我们就从实践的角度用Python的hmmlearn库来学习HMM的使用.关于hmmlearn的更多资料在官方文 ...
- HMM:隐马尔可夫模型HMM
http://blog.csdn.net/pipisorry/article/details/50722178 隐马尔可夫模型 隐马尔可夫模型(Hidden Markov Model,HMM)是统计模 ...
- 机器学习之隐马尔科夫模型HMM(六)
摘要 隐马尔可夫模型(Hidden Markov Model,HMM)是统计模型,它用来描述一个含有隐含未知参数的马尔科夫过程.其难点是从可观察的参数中确定该过程的隐含参数,然后利用这些参数来作进一步 ...
随机推荐
- centos7破解安装confluence5.9.11
应用环境:Confluence是一个专业的企业知识管理与协同软件,也可以用于构建企业wiki.通过它可以实现团队成员之间的协作和知识共享. 安装环境:centos7.3 Java环境 1.7.0_79 ...
- 洛谷P2468 SDOI 2010 粟粟的书架
题意:给你一个矩形书架,每个点是这本书的页数,每次询问(x1,y1)(x2,y2)这个小矩形里最少需要取几本书使得页数和等于Hi. 题解:小数据二位前缀和预处理+二分答案,大数据一行所以用主席树做,感 ...
- poj 3252 Round Numbers(数位dp 处理前导零)
Description The cows, as you know, have no fingers or thumbs and thus are unable to play Scissors, P ...
- 最全面的 Spring 学习笔记
http://www.codeceo.com/article/learn-spring.html 来源:泊浮目 分享到:更多36 Spring致力于提供一种方法管理你的业务对象.在大量Java EE的 ...
- java 判断元素是否在数组内
一,先转为List,再使用contains()方法 String[] strArr = new String[] { "a", "b", "c&quo ...
- 安装PHP ImageMagick笔记
安装过程 $ pecl install imagick 当提示Please provide the prefix of Imagemagick installation [autodetect] :直 ...
- Vim auto-pairs设置选项
let g:AutoPairs = {'(':')', '[':']', '{':'}',"'":"'",'"':'"'} 设置要自动配对的 ...
- 在Vue框架中使用百度地图
1.首先在index.html中引入百度地图 <script type="text/javascript" src="http://api.map.baidu.co ...
- [luogu5077][Tweetuzki 爱等差数列]
题目链接 思路 数学题 首先列出等差数列求和的式子. \[S = \frac{(n + m)(n - m + 1)}{2}(n为末项,m为首项)\] \[S * 2= (n + m)(n - m + ...
- Flask Mysql数据库连接
下载库: pip install flask-sqlalchemy 下载后进入终端使用python后import导入模块测试没有报错就说明成功了 py文件: # -*- encoding: utf-8 ...
