机器学习入门14 - 神经网络简介 (Introduction to Neural Networks)

原文链接：https://developers.google.com/machine-learning/crash-course/introduction-to-neural-networks/

神经网络是更复杂版本的特征组合。实质上，神经网络会学习适合相应特征组合。

1- 剖析

“非线性问题”意味着无法使用形式为“$b + w_1x_1 + w_2x_2$”的线性模型准确预测标签。
对非线性问题可以用特征组合的方法进行建模。

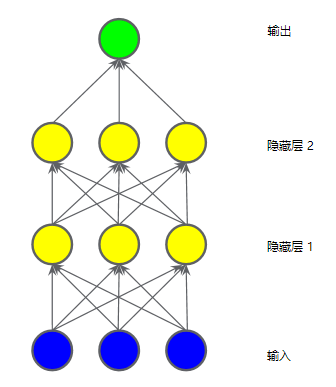
隐藏层

“隐藏层”表示中间值。
如果构建一个多层模型，“隐藏层”每个节点是上一层输入节点值的加权和，输出是“隐藏层”节点的加权和，那么此模型仍是线性的。
因为当将输出表示为输入的函数并进行简化时，只是获得输入的另一个加权和而已。
       

激活函数

要对非线性问题进行建模，可以直接引入非线性函数。
可以用非线性函数将每个隐藏层节点像管道一样连接起来。
在隐藏层中的各个节点的值传递到下一层进行加权求和之前，采用一个非线性函数对其进行了转换，这种非线性函数称为激活函数。
       
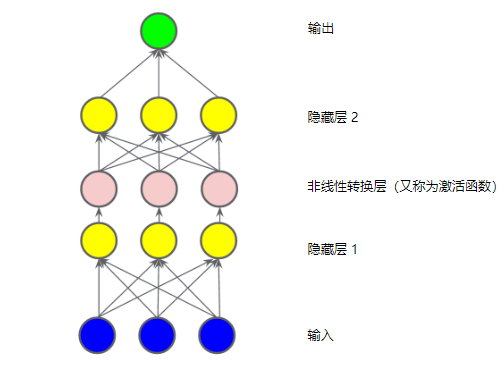
通过在非线性上堆叠非线性，能够对输入和预测输出之间极其复杂的关系进行建模。
简而言之，每一层均可通过原始输入有效学习更复杂、更高级别的函数。

常见激活函数

S型激活函数

S型激活函数将加权和转换为介于 0 和 1 之间的值。
S 型函数的响应性在两端相对较快地减少。
公式：
       $F(x)=\frac{1} {1+e^{-x}}$
曲线图：
      

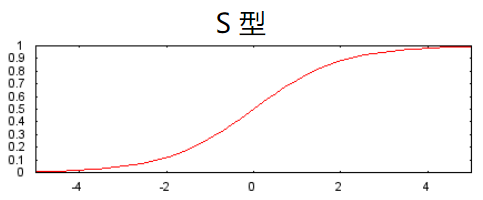
修正线性单元激活函数（简称为 ReLU）

ReLU 的优势:基于实证发现（可能由 ReLU 驱动），拥有更实用的响应范围。
相较于 S 型函数等平滑函数，效果通常要好一点，同时还非常易于计算。
公式：
        $F(x)=max(0,x)$
曲线图：
       

其他激活函数

实际上，所有数学函数均可作为激活函数。
TensorFlow 为各种激活函数提供开箱即用型支持。建议从 ReLU 着手。

2- 总结

通常所说的“神经网络”的所有标准组件：

• 一组节点，类似于神经元，位于层中。
• 一组权重，表示每个神经网络层与其下方的层之间的关系。下方的层可能是另一个神经网络层，也可能是其他类型的层。
• 一组偏差，每个节点一个偏差。
• 一个激活函数，对层中每个节点的输出进行转换。不同的层可能拥有不同的激活函数。

3- 练习

xxx

4- 关键词

激活函数 (activation function)
一种函数（例如 ReLU 或 S 型函数），用于对上一层的所有输入求加权和，然后生成一个输出值（通常为非线性值），并将其传递给下一层。

隐藏层 (hidden layer)
神经网络中的合成层，介于输入层（即特征）和输出层（即预测）之间。神经网络包含一个或多个隐藏层。

神经网络 (neural network)
一种模型，灵感来源于脑部结构，由多个层构成（至少有一个是隐藏层），每个层都包含简单相连的单元或神经元（具有非线性关系）。

神经元 (neuron)
神经网络中的节点，通常会接收多个输入值并生成一个输出值。
神经元通过将激活函数（非线性转换）应用于输入值的加权和来计算输出值。

修正线性单元 (ReLU, Rectified Linear Unit)
一种激活函数，其规则如下：

• • 如果输入为负数或 0，则输出 0。
  • 如果输入为正数，则输出等于输入。

S 型函数 (sigmoid function)
一种函数，可将逻辑回归输出或多项回归输出（对数几率）映射到概率，以返回介于 0 到 1 之间的值。
S 型函数的公式：$y = \frac{1}{1 + e^{-\sigma}}$
在逻辑回归问题中， $\sigma$非常简单：$\sigma = b + w_1x_1 + w_2x_2 + … w_nx_n$
换句话说，S 型函数可将$\sigma$转换为介于 0 到 1 之间的概率。
在某些神经网络中，S 型函数可作为激活函数使用。