本文根据《大话数据结构》一书，实现了Java版的二叉排序树/二叉搜索树。

二叉排序树介绍

在上篇博客中，顺序表的插入和删除效率还可以，但查找效率很低；而有序线性表中，可以使用折半、插值、斐波那契等查找方法来实现，但因为要保持有序，其插入和删除操作很耗费时间。

二叉排序树(Binary Sort Tree)，又称为二叉搜索树，则可以在高效率的查找下，同时保持插入和删除操作也又较高的效率。下图为典型的二叉排序树。

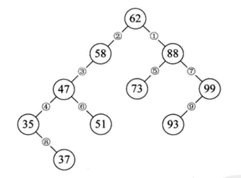
二叉查找树具有以下性质：

　　(1) 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

　　(2) 任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

　　(3) 任意节点的左、右子树也分别为二叉查找树。

查找操作

思路：查找值与结点数据对比，根据大小确定往左子树还是右子树进行下一步比较。

采用递归的查找算法

  1. 	/*
  2. 	 * 查找
  3. 	 */
  4. 	public boolean SearchBST(int key) {
  5. 		return SearchBST(key, root);
  6. 	}
  7.  
  8. 	private boolean SearchBST(int key, Node node) {
  9. 		if (node == null)
  10. 			return false;
  11. 		if (node.data == key) {
  12. 			return true;
  13. 		} else if (node.data < key) {
  14. 			return SearchBST(key, node.rChild);
  15. 		} else {
  16. 			return SearchBST(key, node.lChild);
  17. 		}
  18. 	}

　

采用非递归的查找算法

  1. 	/*
  2. 	 * 查找，非递归
  3. 	 */
  4. 	public boolean SearchBST2(int key) {
  5. 		Node p = root;
  6. 		while (p != null) {
  7. 			if (p.data > key) {
  8. 				p = p.lChild;
  9. 			} else if (p.data < key) {
  10. 				p = p.rChild;
  11. 			} else {
  12. 				return true;
  13. 			}
  14. 		}
  15. 		return false;
  16. 	}

　　

插入操作

思路：与查找类似，但需要一个父节点来进行赋值。

采用非递归的插入算法：

  1. 	/*
  2. 	 * 插入，自己想的，非递归
  3. 	 */
  4. 	public boolean InsertBST(int key) {
  5. 		Node newNode = new Node(key);
  6. 		if (root == null) {
  7. 			root = newNode;
  8. 			return true;
  9. 		}
  10. 		Node f = null; // 指向父结点
  11. 		Node p = root; // 当前结点的指针
  12. 		while (p != null) {
  13. 			if (p.data > key) {
  14. 				f = p;
  15. 				p = p.lChild;
  16. 			} else if (p.data < key) {
  17. 				f = p;
  18. 				p = p.rChild;
  19. 			} else {
  20. 				System.out.println("树中已有相同数据，不再插入！");
  21. 				return false;
  22. 			}
  23. 		}
  24. 		if (f.data > key) {
  25. 			f.lChild = newNode;
  26. 		} else if (f.data < key) {
  27. 			f.rChild = newNode;
  28. 		}
  29. 		return true;
  30. 	}

　　

采用递归的插入算法：

  1. 	/*
  2. 	 * 插入，参考别人博客，递归
  3. 	 * 思路：把null情况排除后用递归，否则无法赋值
  4. 	 */
  5. 	public boolean InsertBST2(int key) {
  6. 		if (root == null) {
  7. 			root = new Node(key);
  8. 			return true;
  9. 		}
  10. 		return InsertBST2(key, root);
  11. 	}
  12.  
  13. 	private boolean InsertBST2(int key, Node node) {
  14. 		if (node.data > key) {
  15. 			if (node.lChild == null) {
  16. 				node.lChild = new Node(key);
  17. 				return true;
  18. 			} else {
  19. 				return InsertBST2(key, node.lChild);
  20. 			}
  21. 		} else if (node.data < key) {
  22. 			if (node.rChild == null) {
  23. 				node.rChild = new Node(key);
  24. 				return true;
  25. 			} else {
  26. 				return InsertBST2(key, node.rChild);
  27. 			}
  28. 		} else {
  29. 			System.out.println("树中已有相同数据，不再插入！");
  30. 			return false;
  31. 		}
  32. 	}

新补充：在写【Java】 大话数据结构(12) 查找算法(3) （平衡二叉树（AVL树））这篇博客时，发现以下的插入方法比较好（如果没有要求返回值必须为boolean格式的话）：（推荐使用此类方法）

  1. 	/*
  2. 	 * 插入操作
  3. 	 */
  4. 	public void insert(int key) {
  5. 		root = insert(root, key);
  6. 	}
  7.  
  8. 	private Node insert(Node node, int key) {
  9. 		if (node == null) {
  10. 			// System.out.println("插入成功！");
  11. 			// 也可以定义一个布尔变量来保存插入成功与否
  12. 			return new Node(key);
  13. 		}
  14. 		if (key == node.data) {
  15. 			System.out.println("数据重复，无法插入！");
  16. 		} else if (key < node.data) {
  17. 			node.lChild=insert(node.lChild, key);
  18. 		} else {
  19. 			node.rChild=insert(node.rChild, key);
  20. 		}
  21. 		return node;
  22. 	}

　　

删除操作

思路：

（1）删除叶子结点

　　直接删除；

（2）删除仅有左或右子树的结点

　　子树移动到删除结点的位置即可；

（3）删除左右子树都有的结点

　　找到删除结点p的直接前驱（或直接后驱）s，用s来替换结点p，然后删除结点s，如下图所示。

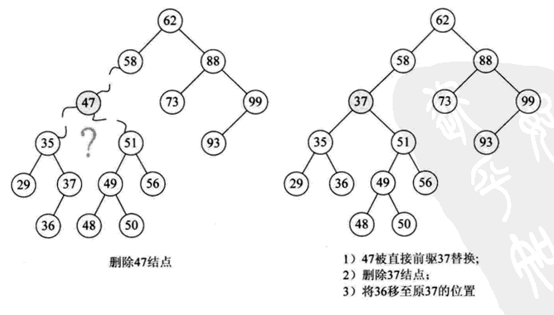
首先找到删除结点位置及其父结点

  1. 	/*
  2. 	 * 删除操作，先找到删除结点位置及其父结点
  3. 	 * 因为需要有父结点，所以暂时没想到递归的方法（除了令Node对象带个parent属性）
  4. 	 */
  5. 	public boolean deleteBST(int key) {
  6. 		if (root == null) {
  7. 			System.out.println("空表，删除失败");
  8. 			return false;
  9. 		}
  10. 		Node f = null; // 指向父结点
  11. 		Node p = root; // 指向当前结点
  12. 		while (p != null) {
  13. 			if (p.data > key) {
  14. 				f = p;
  15. 				p = p.lChild;
  16. 			} else if (p.data < key) {
  17. 				f = p;
  18. 				p = p.rChild;
  19. 			} else {
  20. 				delete(p, f);
  21. 				return true;
  22. 			}
  23. 		}
  24. 		System.out.println("该数据不存在");
  25. 		return false;
  26. 	}

　　

再根据上述思路进行结点p的删除：（需注意删除结点为根节点的情况）

  1. 	/*
  2. 	 * 删除结点P的操作
  3. 	 * 必须要有父结点,因为Java无法直接取得变量p的地址（无法使用*p=(*p)->lChild）
  4. 	 */
  5. 	private void delete(Node p, Node f) {// p为删除结点，f为其父结点
  6. 		if (p.lChild == null) { // 左子树为空，重接右子树
  7. 			if (p == root) { // 被删除结点为根结点时，无法利用f，该情况不能忽略
  8. 				root = root.rChild;
  9. 				p = null;
  10. 			} else {
  11. 				if (f.data > p.data) { // 被删结点为父结点的左结点，下同
  12. 					f.lChild = p.rChild;
  13. 					p = null; // 释放结点别忘了
  14. 				} else {// 被删结点为父结点的右结点，下同
  15. 					f.rChild = p.rChild;
  16. 					p = null;
  17. 				}
  18. 			}
  19. 		} else if (p.rChild == null) { // 右子树为空，重接左子树
  20. 			if (p == root) { // 被删除结点为根结点
  21. 				root = root.lChild;
  22. 				p = null;
  23. 			} else {
  24. 				if (f.data > p.data) {
  25. 					f.lChild = p.lChild;
  26. 					p = null;
  27. 				} else {
  28. 					f.rChild = p.lChild;
  29. 					p = null;
  30. 				}
  31. 			}
  32. 		} else { // 左右子树都不为空,删除位置用前驱结点替代
  33. 			Node q, s;
  34. 			q = p;
  35. 			s = p.lChild;
  36. 			while (s.rChild != null) { // 找到待删结点的最大前驱s
  37. 				q = s;
  38. 				s = s.rChild;
  39. 			}
  40. 			p.data = s.data; // 改变p的data就OK
  41. 			if (q != p) {
  42. 				q.rChild = s.lChild;
  43. 			} else {
  44. 				q.lChild = s.lChild;
  45. 			}
  46. 			s = null;
  47. 		}
  48. 	}

　　

　　

完整代码（含测试代码）

  1. package BST;
  2.  
  3. /**
  4.  * 二叉排序树（二叉查找树）
  5.  * 若是泛型，则要求满足T extends Comparable<T> static问题
  6.  * @author Yongh
  7.  *
  8.  */
  9. class Node {
  10. 	int data;
  11. 	Node lChild, rChild;
  12.  
  13. 	public Node(int data) {
  14. 		this.data = data;
  15. 		lChild = null;
  16. 		rChild = null;
  17. 	}
  18. }
  19.  
  20. public class BSTree {
  21. 	private Node root;
  22.  
  23. 	public BSTree() {
  24. 		root = null;
  25. 	}
  26.  
  27. 	/*
  28. 	 * 查找
  29. 	 */
  30. 	public boolean SearchBST(int key) {
  31. 		return SearchBST(key, root);
  32. 	}
  33.  
  34. 	private boolean SearchBST(int key, Node node) {
  35. 		if (node == null)
  36. 			return false;
  37. 		if (node.data == key) {
  38. 			return true;
  39. 		} else if (node.data < key) {
  40. 			return SearchBST(key, node.rChild);
  41. 		} else {
  42. 			return SearchBST(key, node.lChild);
  43. 		}
  44. 	}
  45.  
  46. 	/*
  47. 	 * 查找，非递归
  48. 	 */
  49. 	public boolean SearchBST2(int key) {
  50. 		Node p = root;
  51. 		while (p != null) {
  52. 			if (p.data > key) {
  53. 				p = p.lChild;
  54. 			} else if (p.data < key) {
  55. 				p = p.rChild;
  56. 			} else {
  57. 				return true;
  58. 			}
  59. 		}
  60. 		return false;
  61. 	}
  62.  
  63. 	/*
  64. 	 * 插入，自己想的，非递归
  65. 	 */
  66. 	public boolean InsertBST(int key) {
  67. 		Node newNode = new Node(key);
  68. 		if (root == null) {
  69. 			root = newNode;
  70. 			return true;
  71. 		}
  72. 		Node f = null; // 指向父结点
  73. 		Node p = root; // 当前结点的指针
  74. 		while (p != null) {
  75. 			if (p.data > key) {
  76. 				f = p;
  77. 				p = p.lChild;
  78. 			} else if (p.data < key) {
  79. 				f = p;
  80. 				p = p.rChild;
  81. 			} else {
  82. 				System.out.println("数据重复，无法插入！");
  83. 				return false;
  84. 			}
  85. 		}
  86. 		if (f.data > key) {
  87. 			f.lChild = newNode;
  88. 		} else if (f.data < key) {
  89. 			f.rChild = newNode;
  90. 		}
  91. 		return true;
  92. 	}
  93.  
  94. 	/*
  95. 	 * 插入，参考别人博客，递归
  96. 	 * 思路：类似查找，
  97. 	 *       但若方法中的node为null的话，将无法插入新数据，需排除null的情况
  98. 	 */
  99. 	public boolean InsertBST2(int key) {
  100. 		if (root == null) {
  101. 			root = new Node(key);
  102. 			return true;
  103. 		}
  104. 		return InsertBST2(key, root);
  105. 	}
  106.  
  107. 	private boolean InsertBST2(int key, Node node) {
  108. 		if (node.data > key) {
  109. 			if (node.lChild == null) { // 有null的情况下，才有父结点
  110. 				node.lChild = new Node(key);
  111. 				return true;
  112. 			} else {
  113. 				return InsertBST2(key, node.lChild);
  114. 			}
  115. 		} else if (node.data < key) {
  116. 			if (node.rChild == null) {
  117. 				node.rChild = new Node(key);
  118. 				return true;
  119. 			} else {
  120. 				return InsertBST2(key, node.rChild);
  121. 			}
  122. 		} else {
  123. 			System.out.println("数据重复，无法插入！");
  124. 			return false;
  125. 		}
  126. 	}
  127.  
  128. 	/*
  129. 	 * 这样的插入是错误的（node无法真正被赋值）
  130. 	 */
  131. 	/*
  132. 	private boolean InsertBST2(int key, Node node) {
  133. 		if(node!=null) {
  134. 			if (node.data > key)
  135. 				return InsertBST2(key, node.lChild);
  136. 			else if (node.data < key)
  137. 				return InsertBST2(key, node.rChild);
  138. 			else
  139. 				return false;//重复
  140. 		}else {
  141. 			node=new Node(key);
  142. 			return true;
  143. 		}
  144. 	}
  145. 	*/
  146.  
  147. 	/*
  148. 	 * 删除操作，先找到删除结点位置及其父结点
  149. 	 * 因为需要有父结点，所以暂时没想到递归的方法（除了令Node对象带个parent属性）
  150. 	 */
  151. 	public boolean deleteBST(int key) {
  152. 		if (root == null) {
  153. 			System.out.println("空表，删除失败");
  154. 			return false;
  155. 		}
  156. 		Node f = null; // 指向父结点
  157. 		Node p = root; // 指向当前结点
  158. 		while (p != null) {
  159. 			if (p.data > key) {
  160. 				f = p;
  161. 				p = p.lChild;
  162. 			} else if (p.data < key) {
  163. 				f = p;
  164. 				p = p.rChild;
  165. 			} else {
  166. 				delete(p, f);
  167. 				System.out.println("删除成功！");
  168. 				return true;
  169. 			}
  170. 		}
  171. 		System.out.println("该数据不存在");
  172. 		return false;
  173. 	}
  174.  
  175. 	/*
  176. 	 * 删除结点P的操作
  177. 	 * 必须要有父结点,因为Java无法直接取得变量p的地址（无法使用*p=(*p)->lChild）
  178. 	 */
  179. 	private void delete(Node p, Node f) {// p为删除结点，f为其父结点
  180. 		if (p.lChild == null) { // 左子树为空，重接右子树
  181. 			if (p == root) { // 被删除结点为根结点，该情况不能忽略
  182. 				root = root.rChild;
  183. 				p = null;
  184. 			} else {
  185. 				if (f.data > p.data) { // 被删结点为父结点的左结点，下同
  186. 					f.lChild = p.rChild;
  187. 					p = null; // 释放结点别忘了
  188. 				} else {// 被删结点为父结点的右结点，下同
  189. 					f.rChild = p.rChild;
  190. 					p = null;
  191. 				}
  192. 			}
  193. 		} else if (p.rChild == null) { // 右子树为空，重接左子树
  194. 			if (p == root) { // 被删除结点为根结点
  195. 				root = root.lChild;
  196. 				p = null;
  197. 			} else {
  198. 				if (f.data > p.data) {
  199. 					f.lChild = p.lChild;
  200. 					p = null;
  201. 				} else {
  202. 					f.rChild = p.lChild;
  203. 					p = null;
  204. 				}
  205. 			}
  206. 		} else { // 左右子树都不为空,删除位置用前驱结点替代
  207. 			Node q, s;
  208. 			q = p;
  209. 			s = p.lChild;
  210. 			while (s.rChild != null) { // 找到待删结点的最大前驱s
  211. 				q = s;
  212. 				s = s.rChild;
  213. 			}
  214. 			p.data = s.data; // 改变p的data就OK
  215. 			if (q != p) {
  216. 				q.rChild = s.lChild;
  217. 			} else {
  218. 				q.lChild = s.lChild;
  219. 			}
  220. 			s = null;
  221. 		}
  222. 	}
  223.  
  224. 	/*
  225. 	 * 中序遍历
  226. 	 */
  227. 	public void inOrder() {
  228. 		inOrder(root);
  229. 		System.out.println();
  230. 	}
  231.  
  232. 	public void inOrder(Node node) {
  233. 		if (node == null)
  234. 			return;
  235. 		inOrder(node.lChild);
  236. 		System.out.print(node.data + " ");
  237. 		inOrder(node.rChild);
  238. 	}
  239.  
  240. 	/*
  241. 	 * 测试代码
  242. 	 */
  243. 	public static void main(String[] args) {
  244. 		BSTree aTree = new BSTree();
  245. 		BSTree bTree = new BSTree();
  246. 		int[] arr = { 62, 88, 58, 47, 35, 73, 51, 99, 37, 93 };
  247. 		for (int a : arr) {
  248. 			aTree.InsertBST(a);
  249. 			bTree.InsertBST2(a);
  250. 		}
  251. 		aTree.inOrder();
  252. 		bTree.inOrder();
  253. 		System.out.println(aTree.SearchBST(35));
  254. 		System.out.println(bTree.SearchBST2(99));
  255. 		aTree.deleteBST(47);
  256. 		aTree.inOrder();
  257. 	}
  258. }

　　

  1.  
  2. true
  3. true
  4. 删除成功!
  5.

BSTree

 小结（自己编写时的注意点）：

　　查找：操作简单，注意递归的方法没有循环while (p!=null)，而是并列的几个判断；

　　插入：非递归时，要有父结点；递归时，要注意排除null的情况；

　　删除：记住要分两步，第一步找结点位置时也要把父结点带上；第二步删除结点时，要令p=null，还要注意p==root的情况以及q==p的情况。

【Java】 大话数据结构(11) 查找算法(2)（二叉排序树/二叉搜索树）的更多相关文章

  1. Java与算法之(13) - 二叉搜索树

    查找是指在一批记录中找出满足指定条件的某一记录的过程,例如在数组{ 8, 4, 12, 2, 6, 10, 14, 1, 3, 5, 7, 9, 11, 13, 15 }中查找数字15,实现代码很简单 ...

  2. 【Java】 大话数据结构(12) 查找算法(3) （平衡二叉树（AVL树））

    本文根据<大话数据结构>一书及网络资料,实现了Java版的平衡二叉树(AVL树). 平衡二叉树介绍 在上篇博客中所实现的二叉排序树(二叉搜索树),其查找性能取决于二叉排序树的形状,当二叉排 ...

  3. 【数据结构05】红-黑树基础----二叉搜索树（Binary Search Tree）

    目录 1.二分法引言 2.二叉搜索树定义 3.二叉搜索树的CRUD 4.二叉搜索树的两种极端情况 5.二叉搜索树总结 前言 在[算法04]树与二叉树中,已经介绍过了关于树的一些基本概念以及二叉树的前中 ...

  4. LeetCode第[98]题(Java)：Validate Binary Search Tree（验证二叉搜索树）

    题目:验证二叉搜索树 难度:Medium 题目内容: Given a binary tree, determine if it is a valid binary search tree (BST). ...

  5. 看动画学算法之:平衡二叉搜索树AVL Tree

    目录 简介 AVL的特性 AVL的构建 AVL的搜索 AVL的插入 AVL的删除 简介 平衡二叉搜索树是一种特殊的二叉搜索树.为什么会有平衡二叉搜索树呢? 考虑一下二叉搜索树的特殊情况,如果一个二叉搜 ...

  6. 【Java】 大话数据结构(10) 查找算法(1)（顺序、二分、插值、斐波那契查找）

    本文根据<大话数据结构>一书,实现了Java版的顺序查找.折半查找.插值查找.斐波那契查找. 注:为与书一致,记录均从下标为1开始. 顺序表查找 顺序查找  顺序查找(Sequential ...

  7. 【Java】 大话数据结构(13) 查找算法(4) （散列表（哈希表））

    本文根据<大话数据结构>一书,实现了Java版的一个简单的散列表(哈希表). 基本概念 对关键字key,将其值存放在f(key)的存储位置上.由此,在查找时不需比较,只需计算出f(key) ...

  8. Java实现 LeetCode 108 将有序数组转换为二叉搜索树

    108. 将有序数组转换为二叉搜索树 将一个按照升序排列的有序数组,转换为一棵高度平衡二叉搜索树. 本题中,一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1. 示例: ...

  9. [数据结构]——二叉树（Binary Tree）、二叉搜索树（Binary Search Tree）及其衍生算法

    二叉树(Binary Tree)是最简单的树形数据结构,然而却十分精妙.其衍生出各种算法,以致于占据了数据结构的半壁江山.STL中大名顶顶的关联容器--集合(set).映射(map)便是使用二叉树实现 ...

随机推荐

  1. HTTP 返回的状态码 != 200 ，浏览器不会将返回的内容缓存到本地磁盘上

    今天无意发现的,以前处理HTTP State = 404或403之类的,都是直接返回 HTTP 200 OK,然后加一个缓存设置,例如: Cache-Control: max-age=3600 最近修 ...

  2. Debian8 系统修改语言设置成英文

    本文摘自 https://wiki.debian.org/ChangeLanguage ,感谢作者 * First, you have to set environment variables suc ...

  3. 自己写的一个Vue

    下面这里是我自己写的一个小型的vue,原理就是proxy: //Proxy天生没有prototype,因此要加上,不然extends会报错 Proxy.prototype = Proxy.protot ...

  4. angularJs的继承

    为什么要继承,本来是后端的概念,但是同样适用于前端开发.继承,无疑是将通用的东西抽取出来. 下面介绍的是angular的伪继承,就是说是通过继承scope这个变量来实现的.代码很简单,一行代码就可以. ...

  5. Centos 7和 Centos 6开放查看端口 防火墙关闭打开

    Centos 7 firewall 命令: 查看已经开放的端口: firewall-cmd --list-ports 开启端口 firewall-cmd --zone=public --add-por ...

  6. 数学：拓展Lucas定理

    拓展Lucas定理解决大组合数取模并且模数为任意数的情况 大概的思路是把模数用唯一分解定理拆开之后然后去做 然后要解决的一个子问题是求模质数的k次方 将分母部分转化成逆元再去做就好了 这里贴一份别人的 ...

  7. SQL语句（七）简单查询

    --简单信息查询 --例1 查询所有学生的信息 --学生 -- Student --所有学生 -- 不限定班级.性别.年龄等条件 --所有信息 -- 所有字段,* select * from stud ...

  8. 40个新鲜的 jQuery 插件，使您的网站用户友好

    作为最流行的 JavaScript 开发框架,jQuery 在现在的 Web 开发项目中扮演着重要角色,它简化了 HTML 文档遍历,事件处理,动画以及 Ajax 交互,这篇文章特别收集了40个新鲜的 ...

  9. 【LibreOJ】#6354. 「CodePlus 2018 4 月赛」最短路 异或优化建图+Dijkstra

    [题目]#6354. 「CodePlus 2018 4 月赛」最短路 [题意]给定n个点,m条带权有向边,任意两个点i和j还可以花费(i xor j)*C到达(C是给定的常数),求A到B的最短距离.\ ...

  10. HDU 2049 不容易系列之(4)——考新郎 （错排+组合）

    题目链接. Problem Description 国庆期间,省城HZ刚刚举行了一场盛大的集体婚礼,为了使婚礼进行的丰富一些,司仪临时想出了有一个有意思的节目,叫做"考新郎",具体 ...