程序员必知的8大排序(二)-------简单选择排序，堆排序（java实现）

程序员必知的8大排序(一)-------直接插入排序，希尔排序（java实现）

程序员必知的8大排序(二)-------简单选择排序，堆排序（java实现）

程序员必知的8大排序(三)-------冒泡排序，快速排序（java实现）

程序员必知的8大排序(四)-------归并排序，基数排序（java实现）

程序员必知的8大排序(五)-------总结

3.简单选择排序

（1）基本思想：在要排序的一组数中，选出最小的一个数与第一个位置的数交换；

然后在剩下的数当中再找最小的与第二个位置的数交换，如此循环到倒数第二个数和最后一个数比较为止。

（2）选择排序的时间复杂度：简单选择排序的比较次数与序列的初始排序无关。 假设待排序的序列有 N 个元素，则比较次数永远都是N (N - 1) / 2（和冒泡一样）。而移动次数与序列的初始排序有关。当序列正序时，移动次数最少，为 0。当序列反序时，移动次数最多，为3N (N - 1) /  2。

所以，综上，简单排序的时间复杂度为 O(N2)。

（3）实例：

（3）用java实现

public class Sort {

    public static void main(String[] args) {
        //        int[] arr={3,1,4,2};
        selectSort();
        //        for(int i = 0; i<arr.length; i++){
        //            System.out.println(arr[i]);
        //        }
    }

    public static  void selectSort(){  

        int a[]={1,54,6,3,78,34,12,45};  

        int position=0;  

        for(int i=0;i<a.length;i++){  

            int j=i+1;
            position=i;
            int temp=a[i];
            for(;j<a.length;j++){
                if(a[j]<temp){
                    temp=a[j];
                    position=j;
                }
            }
            a[position]=a[i];
            a[i]=temp;
        }  

        for(int i=0;i<a.length;i++)
            System.out.println(a[i]);
    }  

}

4，堆排序

（1）基本思想：堆排序是一种树形选择排序，是对直接选择排序的有效改进。

堆的定义如下：具有n个元素的序列（h1,h2,...,hn),当且仅当满足（hi>=h2i,hi>=2i+1）或（hi<=h2i,hi<=2i+1）(i=1,2,...,n/2)时称之为堆。在这里只讨论满足前者条件的堆。由堆的定义可以看出，堆顶元素（即第一个元素）必为最大项（大顶堆）。完全二叉树可以很直观地表示堆的结构。堆顶为根，其它为左子树、右子树。初始时把要排序的数的序列看作是一棵顺序存储的二叉树，调整它们的存储序，使之成为一个堆，这时堆的根节点的数最大。然后将根节点与堆的最后一个节点交换。然后对前面(n-1)个数重新调整使之成为堆。依此类推，直到只有两个节点的堆，并对它们作交换，最后得到有n个节点的有序序列。从算法描述来看，堆排序需要两个过程，一是建立堆，二是堆顶与堆的最后一个元素交换位置。所以堆排序有两个函数组成。一是建堆的渗透函数，二是反复调用渗透函数实现排序的函数。

（2）实例：

初始序列：46,79,56,38,40,84

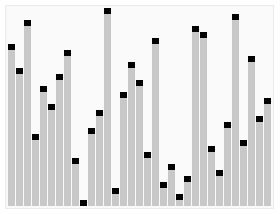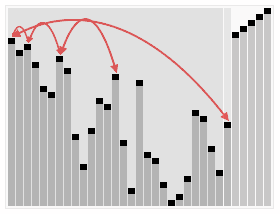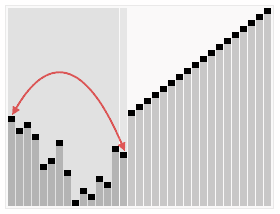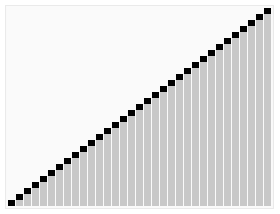
建堆：

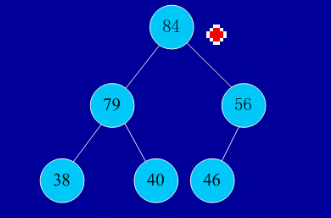
交换，从堆中踢出最大数

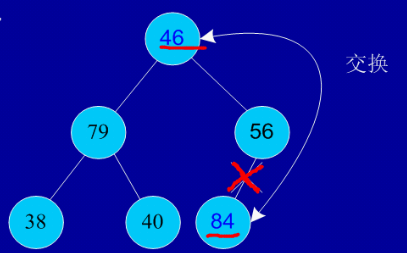
剩余结点再建堆，再交换踢出最大数

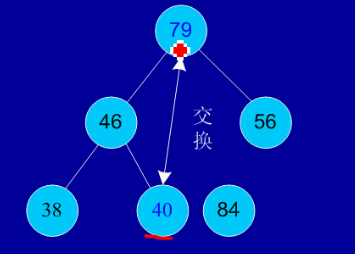
依次类推：最后堆中剩余的最后两个结点交换，踢出一个，排序完成。

（3）用java实现

import java.util.Arrays;

public class Sort {

    public static void main(String[] args) {
        int a[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,56,17,18,23,34,15,35,25,53,51};
        heapSort(a);
    }

    public  static void heapSort(int[] a){

        System.out.println("开始排序");

        int arrayLength=a.length;

        //循环建堆

        for(int i=0;i<arrayLength-1;i++){

            //建堆

            buildMaxHeap(a,arrayLength-1-i);

            //交换堆顶和最后一个元素

            swap(a,0,arrayLength-1-i);

            System.out.println(Arrays.toString(a));

        }

    }

    private  static void swap(int[] data, int i, int j) {

        // TODO Auto-generated method stub

        int tmp=data[i];

        data[i]=data[j];

        data[j]=tmp;

    }

    //对data数组从0到lastIndex建大顶堆

    private static void buildMaxHeap(int[] data, int lastIndex) {

        // TODO Auto-generated method stub

        //从lastIndex处节点（最后一个节点）的父节点开始

        for(int i=(lastIndex-1)/2;i>=0;i--){

            //k保存正在判断的节点

            int k=i;

            //如果当前k节点的子节点存在

            while(k*2+1<=lastIndex){

                //k节点的左子节点的索引

                int biggerIndex=2*k+1;

                //如果biggerIndex小于lastIndex，即biggerIndex+1代表的k节点的右子节点存在

                if(biggerIndex<lastIndex){

                    //若果右子节点的值较大

                    if(data[biggerIndex]<data[biggerIndex+1]){

                        //biggerIndex总是记录较大子节点的索引

                        biggerIndex++;

                    }

                }

                //如果k节点的值小于其较大的子节点的值

                if(data[k]<data[biggerIndex]){

                    //交换他们

                    swap(data,k,biggerIndex);

                    //将biggerIndex赋予k，开始while循环的下一次循环，重新保证k节点的值大于其左右子节点的值

                    k=biggerIndex;

                }else{

                    break;

                }

            }

        }

    }

}