标准误(Standard Error)

sklearn实战-乳腺癌细胞数据挖掘

https://study.163.com/course/introduction.htm?courseId=1005269003&utm_campaign=commission&utm_source=cp-400000000398149&utm_medium=share

1.标准误概念

标准误是数据统计的重点概念，且难以理解。百度上文章缺乏详细描述的文章。所以写下此文让读者能够彻彻底底了解标准误概念。

标准误全称：样本均值的标准误(Standard Error for the Sample Mean),顾名思义，标准误是用于衡量样本均值和总体均值的差距。

2.标准误意义：

用于衡量样本均值和总体均值的差距有多大？

标准误越小----样本均值和总体均值差距越小

标准误越大----样本均值和总体均值差距越大

标准误用于预测样本数据准确性 ，标准误越小，样本均值和总体均值差距越小，样本数据越能代表总体数据。

3.标准误与标准差区别：

对一个总体多次抽样，每次样本大小都为n，那么每个样本都有自己的平均值，这些平均值的标准差叫做标准误。

标准差是单次抽样得到的，用单次抽样得到的标准差可以估计多次抽样才能得到的标准误差

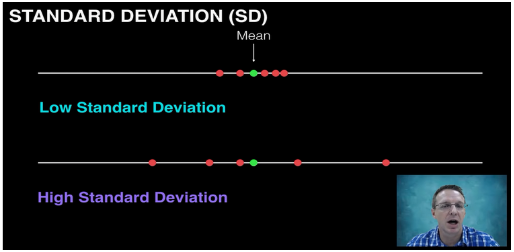
标准差表示数据离散程度：

标准差越大，分布越广，集中程度越差，均值代表性越差

标准差越小，分布集中在平均值附近，均值代表性更好

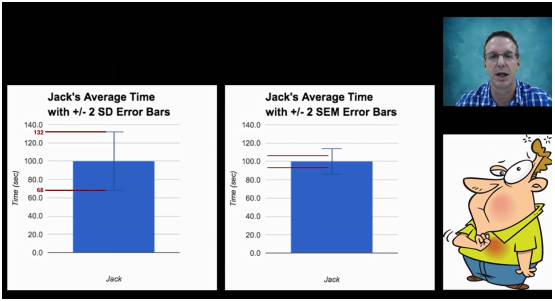
标准差与标准误不同应用范围：
标准差：（图左）在正负两个标准差（95%概率下），Jack消耗时间在68-132秒之间。
标准误：（图右）在正负两个标准误，Jack消耗平均时间大约在95-105秒之间。

4.标准误计算例子

什么是真实的标准误？举个例子，对一个总体12次抽样，生成12个样本，每个样本大小都为5。那么每个样本都有自己的平均值，这些平均值的标准差叫做标准误差。这里就是对表格最后一行数组计算标准差（100，101,99,114,103.....93），最后算出来标准误结果为6.33。

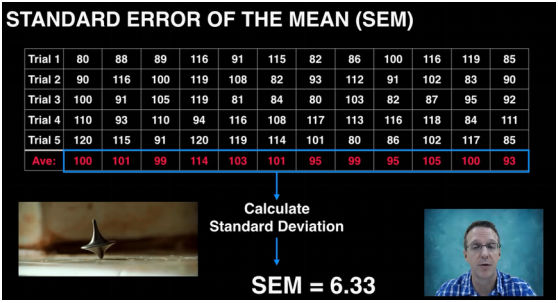
但是为了得到标准误，我们不可能做很多次科学实验。实际上我们可以做一次样本实验，然后采用估算公式：

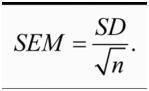
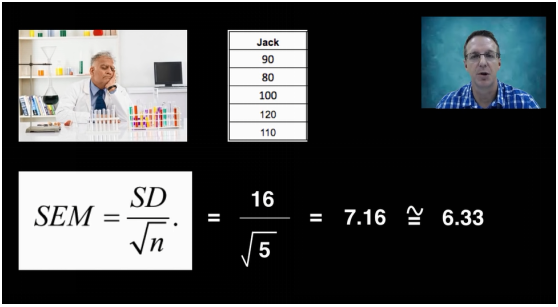
如下图，我们用第一组样本估算真实标准误，此样本标准差除以根号n,结果为7.16， 然后把7.16约等为真实的标准误6.33。

所以标准误也是另外一种形式的标准差，标准误和总体标准差既有相似处，又有区别。标准误是一个比较难得概念，读者一次不能很好理解，如果反复看此文章，然后自己动手程序模拟，就会增强直观印象，加深理解。

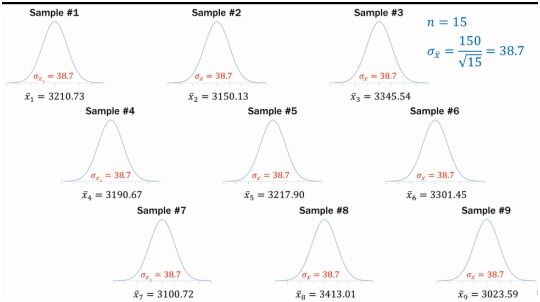
所有的随机样本中，如果数量相同，它们的标准误默认为近似相同（非真正相同）

5.标准误的应用
我们有两组数据，一组观看了指导视频，一组没有观看指导视频，比较两组数据在得分方面有无显著差异？

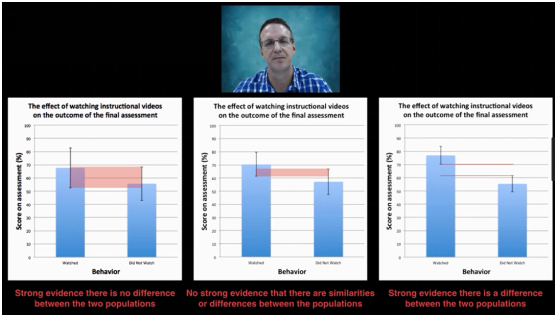
随着样本量不同，我们得到的结果不同。图左，两组数据没有区别，图中两组数据可能有区别，可能没有；图右两组数据有区别
样本量为3时，看视频组的2*标准误为15，没看视频的2*标准误为13。

样本量小时，标准误很大，样本均值和总体均值差异很大，样本数据的代表性很差。

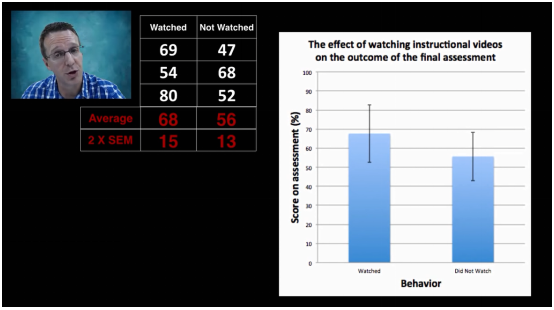
样本量为5时，看视频组的2*标准误为9，没看视频的2*标准误为10。

样本量增大后，标准误变小。

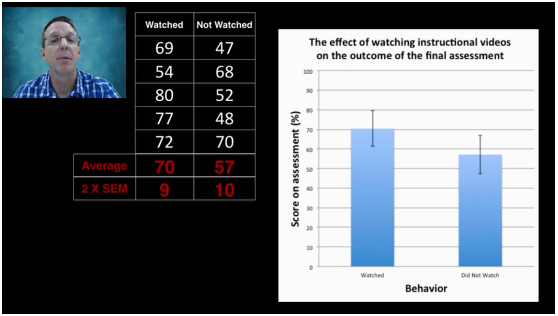
样本量为10时，看视频组的2*标准误为7，没看视频的2*标准误为6。
样本量增大后，标准误再次变小

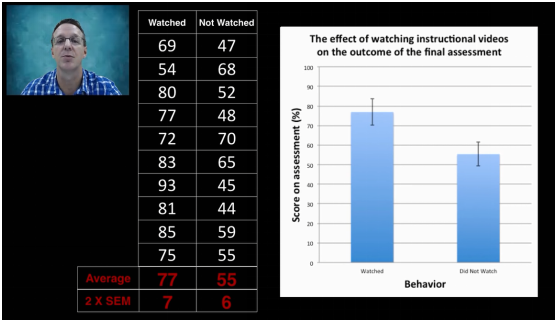
随着样本量不同，我们得到的结果不同。下面的图左（样本量为3），两组数据没有区别，图中（样本量为5）两组数据可能有区别，可能没有；图右（样本量为10）两组数据有区别
实际上，众多毕业论文和专业期刊的统计分析都是错的，虽有华丽的可视化图表，但新手很容易因样本量太小得到错误结果。

6.蒙特卡洛模拟

蒙特卡洛验证，对一组样本进行标准误评估，看公式SE = s/√(n)是否准确

结果表明SE = s/√(n)公式得到的标准误和真实标准误非常接近

样本值100，标准误很小，大约0.1

样本值10，标准误增大，大约0.33

样本值5，标准误再次增大，大约0.45

源代码如下

问题反馈邮箱231469242@qq.com

# -*- coding: utf-8 -*-

import random,math

import numpy as np

n=1000

normal_population=list(np.random.normal(size=n))

mean_population=np.mean(normal_population)

#总体标准差

sigma=np.std(normal_population,ddof=0)

#存放多个随机样本

list_samples=[]

#多个随机样本的平均数

list_samplesMean=[]

#求单个样本估算的标准误

def Standard_error(sample):

std=np.std(sample,ddof=0)

standard_error=std/math.sqrt(len(sample))

return standard_error

#求真实标准误

def Standard_error_real():

for i in range(100):

sample=random.sample(normal_population,100)

list_samples.append(sample)

list_samplesMean=[np.mean(i) for
i in list_samples]

standard_error_real=np.std(list_samplesMean,ddof=0)

return standard_error_real

#plt.hist(normal_values)

#真实标准误

standard_error_real=Standard_error_real()

print(standard_error_real)

#随机抽样

print(Standard_error(list_samples[0]))

print(Standard_error(list_samples[1]))

print(Standard_error(list_samples[2]))

End.

python风控评分卡建模和风控常识

https://study.163.com/course/introduction.htm?courseId=1005214003&utm_campaign=commission&utm_source=cp-400000000398149&utm_medium=share